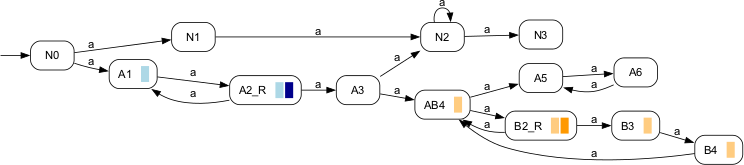Functions on Rabin Automata

RabinLifeStates

Life States w.r.t. Rabin acceptence condition.

Detailed description:

A state is considered life if it allows for a future path such that the acceptance condition is met.

Given a Rabin pair (R,I), the implementation of this function is along the following lines

• initialise the candidate life states L := I

• run a nu-iteration on L to figure the largest existential invariant

• run a mu-iteration on L∩R to restrict L to states which can reach R

• repeat the above two steps until a fix point is attained

• run one more mu-iteration on L to extend to the backward reach

• return L as the result

Depending on the signature, lifeness is required w.r.t. at least one of the provided Rabin pairs.

Example: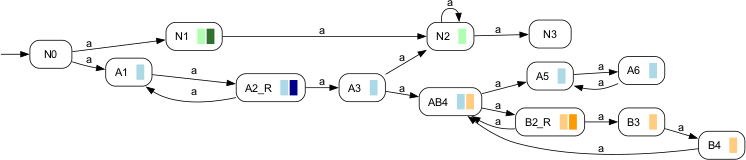

For the blue Rabin pair, the life states are reported as {N0, A1, A2_R}. For the orange Rabin pair, the life states are reported as {N0, A1, A2_R, A3, AB4, B2_R, B3, B4}. For the green Rabin pair, no life states exist.

Applying IsRabinTrim to the above automaton returns false because there exists accessible states, that are not life, e.g., N1

RabinTrim

Delete states that do not contribute to the accepted language.

Detailed description:

Trim a given Rabin automaton RAut by removing states that are not life and/or not accessible; see also RabinLifeStates. The accepted language Rm(RAut) is not affected.

When applied on the example given for RabinLifeStates, RabinTrim returns the result:

Applying IsRabinTrim to the above automaton returns true.

IsRabinTrim

Test for a Rabin automaton to be trim.

Detailed description:

A Rabin automaton is considered trim if all states are accessible and life w.r.t. at least one Rabin pair. In other words, trimness requires all states to contribute to the accepted language. For examples see RabinTrim and RabinLifeStates.

RabinSimplify

Simplify individual Rabin pairs and remove doublets.

Detailed description:

Simplify the acceptance condition of the Rabin automaton RAut by restricting Rabin pairs to life states and removing doublets. The accepted language Rm(RAut) is not affected.

Example:

We use the same automaton as in RabinLifeStates:

Applying RabinSimplify we obtain:

Applying RabinTrim and RabinSimplify we obtain:

Applying IsRabinTrim to the above automaton returns true.

RabinBuechiAutomaton

Assemble an automaton to accept a given Rabin/Buechi accepted lanuage.

Detailed description:

Given a Rabin automaton RAut and a Buechi automaton BAut, compose a Rabin automaton GRes on the product state set. Then lift acceptance conditions such that the Rabin accepted language matches that of RAut and the Buechi accepted language matches that of BAut; i.e., Rm(RAut) = Rm(Gres) and Bm(BAut) = Bm(Gres).

Example:

Component RAut Component BAut

Composition GRes

Parameter Conditions:

Arguments must have matching alphabets Sigma. Arguments must be full, i.e., generate Sigma^w

RabinBuechiProduct

Assemble an automaton to accept the intsection of given Rabuin/Buechi accepted lanuage.

Detailed description:

Given a Rabin automaton RAut and a Buechi automaton BAut, compose a Rabin automaton GRes on the product augmented state set (see BuechiProduct). Set the Rabin acceptance condition such that accepted words are those accepted by both arguments; i.e., Rm(Gres) = Rm(RAut)∩Bm(BAut).

To facilitate controller syhnthesis, we also set the Buechi acceptance to appcept Bm(BAut). This feature requires RAut to be full.

Example:

Component RAut Component BAut

Composition GRes

Parameter Conditions:

Arguments must have matching alphabets Sigma. The argument RAut must be full, i.e., generate Sigma^w