| |
|
||||||
|
|
|||||||
|
Normal SublanguagesFunctions related to the notion of normality and supervision under partial observation Definition of Normality
Given two languages L and K over a common
alphabet Sigma,
and a set of observable events Sigma_o ⊆ Sigma,
K is normal w.r.t (L,Sigma_o) iff
Note that normality implies K ⊆ L. The function IsNormal is provided to test a specified language for normality.
The notion of normality is conveniently used to discuss supervisory control
under partial observation, under the additional assumption that all controllable events are
observable; i.e. Sigma_c ⊆ Sigma_o.
The closed-loop configuration with a plant L ⊆ Sigma*
and a controller Ho ⊆ Sigma_o* can then be modelled by
the synchronous composition
Note that, the condition Sigma_c ⊆ Sigma_o is not a formal prerequisit of the proposed approach. However, the controllers under consideration can only exercise control by disabling events within Sigma_o, and in this sense the approach is restrictive. A synthesis algorithm for controllers without this restriction is presented in [S5]. Controller Synthesis for Supervision under Partial ObservationConsider a plant L ⊆ Sigma*, a specification E ⊆ Sigma*, uncontrollable events Sigma_uc ⊆ Sigma, and, observable events Sigma_o ⊆ Sigma. The task then is to find a prefix closed controller Ho ⊆ Sigma_o*, such that
(1)
L and Ho are non-blocking, i.e.,
Closure(L ∩ Pinv0(Ho)) = Closure(L) ∩ Pinv0(Ho) ;
For any prefix closed controller Ho that satisfies the above conditions, the closed loop K = L || Ho exhibits the following properties:
(a)
K is relatively closed w.r.t. L;
Moreover, if a language K satisfies
(a)-(d), then the controller Ho = P0(Closure(K)) solves
the synthesis problem. Since all of the conditions (a)-(d) are
preserved under arbitrary union, there uniquely exists a supremal closed-loop
behaviour
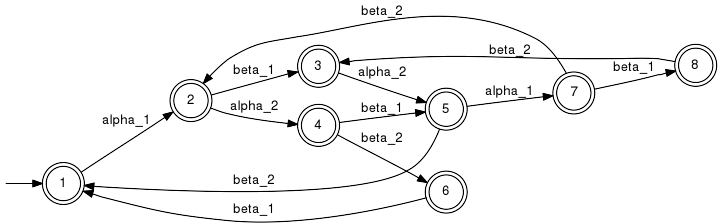
The synthesis plug-in provides the function SupConNorm to compute the supremal closed-loop behaviour. When the plant L and the specification E are prefix closed, condition (a) simplifies to K being closed. Then, SupConNormClosed can be used to compute the supremal closed-loop bahaviour. ExampleConsider the very-simple machine example and assume that all events except from beta_1 are reported to the supervisor, i.e. Sigma_o={alpha_1, alpha_2, beta_2}. Since all controllable events are observable, we define a candidat supervisor Ho ⊆ Sigma_o* by projection, i.e. Ho = P0(Closure(K)). The supervisor Ho, however, will in addition to the events from Sigma_o at any time enable all unobservable events, i.e. beta_1. Thus, the actual closed-loop behaviour under restricted observation is given by Lm(G) ∩ Pinv0(Ho). If Closure(K) happened to be normal w.r.t. (L(G),Sigma_o), the intended closed-loop behaviour would be achieved. However, in our example Closure(K) is not normal w.r.t (L(G),Sigma_o):
Note that the candidate closed loop at state 2 allows machine M2 to pick up a workpiece from the buffer which at that state is empty. This clearly violates the specification. When considering the same scenario but with Sigma_o={alpha_1, beta_1, alpha_2}, i.e. beta_2 is the only unobservable event, in fact Closure(K) turns out to be normal and we have L(G) ∩ Pinv0(Ho) = Closure(K). IsNormalTests normality condition. Signature:IsNormal(+In+ Generator L, +In+ EventSet AObs, +In+ Generator K, +Out+ Boolean BRes) IsNormal(+In+ System GPlant, +In+ Generator GCand, +Out+ Boolean BRes) Detailed description:Tests whether the language K (marked by argument K or GCand) is normal w.r.t. the language L (marked by argument L or GPlant) and the set of observable events. The latter may be given explicitely or is extracted from GPlant. The implementation tests for K ⊇ L ∩ Pinv0(P0(K)), which is necessary for normality. Under the assumption K ⊆ L, the test is also sufficient. Parameter Conditions:Arguments are required to be deterministic. For a necessary and sufficient test, K must mark a subset of the language marked by L. SupNormComputes the supremal normal sublanguage. Signature:SupNorm(+In+ Generator L, +In+ EventSet AObs, +In+ Generator K, +Out+ Generator GRes) SupNorm(+In+ System GPlant, +In+ Generator GCand, +Out+ Generator GRes) Detailed description:
The function SupNorm computes a realisation of the supremal sublanguage
N↑ of K (generated by argument K or GCand)
that is normal w.r.t. L (generated by argument L or GPlant):
The set of observable events Sigma_o
may be given explicitely or is extracted from GPlant.
The implemention evaluates the Lin-Brandt formula for prefix closed
languages L and K, as proposed in [S2]:
Parameter Conditions:Parameters have to be deterministic, the result will be deterministic. K must be a subset of L; While arguments are interpreted as generated languages, the result is given as marked language. SupNormClosedComputes the supremal normal and closed sublanguage. Signature:SupNormClosed(+In+ Generator L, +In+ EventSet AObs, +In+ Generator K, +Out+ Generator GRes) SupNormClosed(+In+ System GPlant, +In+ Generator GCand, +Out+ Generator GRes) Detailed description:
The function SupNormClosed computes a realisation of the
supremal sublanguage N↑ of K (generated by argument K or GCand)
that is normal w.r.t. L (generated by argument L or GPlant) and closed:
The set of observable events Sigma_o
may be given explicitely or is extracted from GPlant.
The implemention evaluates the Lin-Brandt formula for prefix closed
languages, as proposed in [S2]:
Parameter Conditions:Parameters have to be deterministic, result is deterministic. K must be a subset of L. While arguments are interpreted as generated languages, the result is given as marked and generated language. SupConNormClosedComputes the supremal controllable, normal and closed sublanguage. Signature:SupConNormClosed(+In+ Generator L, +In+ EventSet ACtrl, +In+ EventSet AObs, +In+ Generator E, +Out+ Generator GRes) SupConNormClosed(+In+ System GPlant, +In+ Generator GSpec, +Out+ Generator GRes) Detailed description:
The function SupConNormClosed computes a realisation of the supremal controllable, normal
and closed sublanguage
K↑ of the specification E (generated by argument E or GSpec) w.r.t.\
the plant L (generated by argument L or GPlant):
The set of controllable events Sigma_c
and the set of observable events Sigma_o
may be given explicitely or are extracted from GPlant.
The implemention evaluates the following expressions
Example:Consider the very-simple machine example and assume that all events except of beta_1 are observabe, i.e. Sigma_o={alpha_1, alpha_2, beta_2}. The specification requires the supervisor to disable alpha_1 unless the buffer it not known to be empty, and, to disable alpha_2 unless the buffer it not known to be full. Thus, a supervisor may initially enable alpha_1 and disable alpha_2. The plant will then start M1, i.e., it executes alpha_1, to eventually complete the process, indicated by the unobservable event beta_1. However, the only way for the supervisor to figure that the process was completed and that alpha_2 could be enabled would be a subsequent alpha_1. However, the supervisor will not enable alpha_1 unless the buffer is known to be empty, and this will never happen, as long as alpha_2 is disabled. Consequently, the process stops after the sequence alpha_1 beta_1 and SupConNormClosed consistently returns the following
Parameter Conditions:Parameters have to be deterministic, result is deterministic. While arguments are interpreted as generated languages, the result is given as marked and generated language. SupConNormComputes the supremal controllable and normal sublanguage. Signature:SupConNorm(+In+ Generator L, +In+ EventSet ACtrl, +In+ EventSet AObs, +In+ Generator E, +Out+ Generator GRes) SupConNorm(+In+ System GPlant, +In+ Generator GSpec, +Out+ Generator GRes) Detailed description:
The function SupConNorm computes a realisation of the supremal controllable and normal
sublanguage K↑ of the specification E
(marked by argument E or GSpec) w.r.t.
the plant L (marked by argument L or GPlant):
The set of controllable events Sigma_c
and the set of observable events Sigma_o
may be given explicitely or are extracted from the argument GPlant.
The implemention performs the iteration proposed
in [S4]:
If the specification E fails to be relatively marked w.r.t. the plant L,
one may replace E with the supremal sublanguage that is relatively closed
(see also SupRelativelyClosed) before invoking SupConNorm,
to obtain
Remark. The implementation follows the above pseudo code and in addition introduces a Trim operation on the iterate Ki, as proposed in [S4]. In particular, GPlant is technically required to be non-blocking in order for SupConNormClosed to compute the above supremum. If, on the other hand, GPlant is blocking, normality and controllability are achieved w.r.t. the generated language, and one can use the result to obtain a non-blocking supervisor. Example:Consider the very-simple machine example and assume that all events except of beta_1 are observabe, i.e. Sigma_o={alpha_1, alpha_2, beta_2}. As discussed above, the supremal controllable and normal sublanguage (evaluated for the closure of plant and specifications) consists of the string alpha_1 beta_1 and its prefixes. Due to monotonicity of the relevant operators, the supremal controllable and normal sublanguage when evaluated for the marked plant and specification languages must be a subset, and the only such subset within plant and specification consists of the empty string. To obtain a non-trivial result, one may relax the specification by taking its closure and thus don't insist in eventually ending up with an empty buffer. SupConNorm then returns the below
One way to operate both machines with an unobservable event beta_1, is to extend the buffer to have a capacity of two work pieces and to not insist in the buffer to become eventually empty.
Parameter Conditions:Parameters have to be deterministic; result is deterministic. libFAUDES 2.33l --- 2025.09.16 --- with "omegaaut-synthesis-observer-observability-diagnosis-hiosys-iosystem-multitasking-coordinationcontrol-timed-simulator-iodevice-priorities-luabindings-hybrid-example-pybindings" |