• libFAUDES
• Reference  
• Type Index  
• Function Index  
• Literature  
•  
• Sections
• CoreFaudes  
  • CoreFaudes
  • Introduction
  • Generators
  • Alphabets
  • Reachability
  • Boolean Operations
  • Regular Expressions
  • Synchronous Composition
  • Projection
  • StateSet Conversion
  • Elementary Types
  • Miscellaneous
  • Vector Types
• CoordinationControl  
• Diagnosis  
  • Diagnosis
  • Introduction
  • Event-Diagnosis
  • Language-Diagnosis
  • Modular Diagnosis
  • Decentralized Diagnosis
  • Application Example
• Example  
• FaultTolerantControl  
  • FaultTolerantControl
  • Introduction
  • Example
  • Fault-Accommodation
  • Reconfiguration
  • Fault-Patterns
• HioSys  
  • HioSys
  • Introduction
  • Step-By-Step
  • Synthesis Procedure
  • Liveness Properties
  • Application Example
• Hybrid  
• IoSystem  
  • IoSystem
  • Introduction
  • Properties
  • Synthesis
• Multitasking  
  • Multitasking
  • Introduction
  • Functions
  • Observer
  • Optimal Color Set
  • Reachability
  • Synthesis
• Observer  
  • Observer
  • Introduction
  • Verification
  • Synthesis
  • Example
• OmegaAut  
  • OmegaAut
  • Introduction
  • Buechi-Functions
  • Rabin-Functions
  • Buechi-Control
  • Rabin-Control
  • Partial-Obs-Control
• Priorities  
• Simulator  
  • Simulator
  • Introduction
  • Executor Classes
  • Hardware-In-The-Loop
  • IO-Devices
  • Simulator Interconnection
• Synthesis  
  • Synthesis
  • Introduction
  • Controllability
  • Normality
  • Completeness
  • Misc Functions
•  
• Types
• RabinAcceptance  
• RabinAutomaton  
• RabinPair  
•  
• Functions
• BuechiClosure  
• BuechiCon  
• BuechiConNorm  
• BuechiLanguageEquality  
• BuechiLanguageInclusion  
• BuechiParallel  
• BuechiProduct  
• BuechiTrim  
• EpsObservation  
• IsBuechiClosed  
• IsBuechiControllable  
• IsBuechiRelativelyClosed  
• IsBuechiTrim  
• IsRabinTrim  
• PseudoDet  
• RabinBuechiAutomaton  
• RabinBuechiProduct  
• RabinCtrl  
• RabinCtrlPartialObs  
• RabinCtrlPartialObsConsistencyCheck  
• RabinCtrlPartialObsSys  
• RabinCtrlPfx  
• RabinLifeStates  
• RabinSimplify  
• RabinTrim  
• SupBuechiCon  
• SupBuechiConNorm  
• SupRabinCon  
•  

Synthesis w.r.t. Rabin Acceptance

Controller synthesis for non-terminating processes realised by Buechi automata to enforce specifications given as Rabin Automata.

Definition of Omega-Controllability (following [W4b])

The notion of controllability for non-terminating processes used in [W2] nicely covers the case where the specification is relatively closed w.r.t. the plant, but falls short otherwise. This is followed up by [W4b] and we give a concise summary, rephrased in our language based notation.

Consider two omega languages L and K over a common alphabet Sigma, and a set of uncontrollable events Sigma_uc ⊆ Sigma. A finite word s ∈ Sigma is in the controllability prefix of K if there exists an omega language V ⊆ K with s ∈ Prefix(V) such that

(i)    Prefix(V) is *-controllable w.r.t. Prefix(L ∩ sSigma^w), and

(ii)    V is relatively topologically closed w.r.t. L.

The controllability prefix of K is denoted CtrlPfx(K). If the controllability prefix equals the ordinary prefix, then K is said to be omega-controllable w.r.t. (L,Sigma_uc).

To appreciate the above defnition, observe that the two conditions (i) and (ii) imposed on V render V a closed-loop behaviour that can be enforced by a closed controller; see also supervisory control w.r.t. Buechi acceptance. Thus, if for whatever reasons the plant has generated a finite word from the controllability prefix, we could then activate a supervisor that controls the plant to evolve within V ⊆ K. Omega-controllabilty requires that Prefix(K) can at any instance of time be controlled to satisfy K.

Note 1. Omega-controllability in the sense of the above defintion is retained under arbitrary union. Thus,

K↑ := sup{ K ⊆ E | K is omega-controllable w.r.t (L,Sigma_uc) }

is itself omega-controllable. This is not the case for the alternative notion of controllability presented in the context of supervisory control w.r.t. Buechi acceptance. However, the supremal controllable sublanguages w.r.t. either variant of omega controllabily match.

Note 2. The control problem to be addressed is still literaly the same as discussed in the context of supervisory control w.r.t. Buechi acceptance. I.e., given a plant L and a specification E over a common alphabet Sigma = Sigma_c ∪ Sigma_uc, find a closed controller H ⊆ Sigma^w, such that

(a) Prefix(L ∩ H) = Prefix(L) ∩ Prefix(H);

(b) Prefix(H) is *-controllable w.r.t. Prefix(L)

(c) L ∩ H ⊆ E.

If and only if K↑ ≠ 0, there exists a controller with 0 ≠ L ∩ H ⊆ E. Then, such a controller can be extracted from K↑. Hence our interest in the computation of K↑; see also SupRabinCon.

Synthesis Procedure by Example

We illustrate the overall synthesis procedure by reusing a variant of the example presented in the context of Buechi acceptance conditions. Again consider a machine that runs two alternative processes A or B. The processes are initiated by the controllable events a and b, respectively. Once started, a process may terminate with success c or failure d. As a liveness property of the plant, we assume that either process is guaranteed to eventually succeed. This is encoded aa a Buechi acceptance condition.

plant L

For the specification, we use the third vriant, i.e., start with any process A or B, eventually switch to B, and, only on success turn back to A or B. Here, we have encoded the Buechi appeptance condition as a single Rabin pair and have extended the transition structure to a full automaton.

specification E

Taking the RabinBuechiProduct, we obtain a RabinAutomaton that (a) appects the restricted specification E' := E ∩ L by its Rabin acceptance condition and that (b) has a marking to accept the L by its Buechi appectance condition.

candidate K

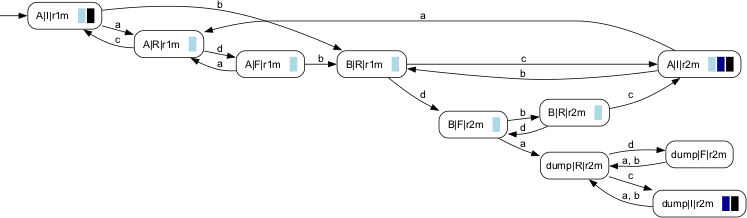
This matches the setting in which [W4a] proposes an algorithm for the computation of the controllability prefix. We apply RabinCtrlPfx to obtain the result as shown below.

CtrlPfx(K) (red marking)

Allthough CtrlPfx(K) ≠ Prefix(K), we observe the empty string to be in CtrlPfx(K). We also note that the only transition that exits CtrlPfx(K) is controllable. This is in general the case. If we restricting the transition structure to generate the supremal closed sublanguages of CtrlPfx(K), the Rabin acceptance condition accepts the supremal omega-controllable sublanguage K↑. Applying SupClosed, we obtain the following result:

K↑

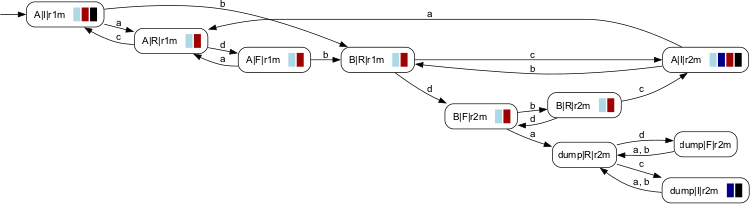
There is also the convenience wrapper SupRabinCon that runs the entire syntheisis procedure as discussed so far.

Recall that in general K↑ can not be achieved as a closed-loop behaviour under a topologically closed controller (i.e., the commonly studied feed-back maps). So, yes, K↑ is the supremal omega-controllable sublanguage of E, but, no, it is not the supremal achievable closed-loop behaviour --- the latter in general does not exist. There are two ways to go about this.

The procedure used for computing the controllability prefix can optionally identify control patterns to be applied to enforce the specification E, or, for that matter, K↑ ⊆ E. Provided that K↑ ≠ 0, the respective control patterns can be recorded and used to set up a controller to achieve a non-empty closed-loop behaviour that satisfies the upper bound K↑. We refer to this control strategy as the greedy controller since it will direct the plant to persistently take the shortest path to once again attain a recurrent Rabin set (R-set of a Rabin pair). The closed-loop behaviour K under greedy control can be computed by RabinCtrl. Formaly, a corresponding H can be obtained by H := Closure(K). For the example at hand, we obtain the following closed-loop behaviour under greedy control.

K [postprocessed with StateMin]

The greedy controller opts for running exclusively the B-process and thereby enforces the specified upper bound E. Obviously this is rather resrictive: by the specification we may to once in a while run the A-process as long as we eventually turn to the B-process. To this end, [W4b] proposes an additional lower-bound specification A and ask for a closed-loop behaviour K with A ⊆ K ⊆ E. For our example we consider the closed langauge generated by the automaton

A'

and propose A := A' ∩ L as the formal lower bound specification. Note that A is by construction reletively closed w.r.t. L. Provided that A ⊆ K↑ [W4b] grants the existence of a closed controller that respects both, the lower bound A and the upper bound E. Under this condition RabinCtrl computes a realisation of an achievable closed-loop behaviour. For our example, we obtain the following.

K [postprocessed with StateMin]

libFAUDES 2.33l --- 2025.09.16 --- with "omegaaut-synthesis-observer-observability-diagnosis-hiosys-iosystem-multitasking-coordinationcontrol-timed-simulator-iodevice-priorities-luabindings-hybrid-example-pybindings"