| |
|
||||||
|
|
|||||||
|
Synchronous CompositionGiven two discrete event systems, the synchronous composition is a discrete event system that models the respective component behaviour under the constraint that shared events must be executed synchronously. Thus, each component restricts the behaviour of the other component.
In terms of languages L1 and L2 over alphabets Sigma1 and
Sigma2, respectively, the resulting behaviour is defined
Note. If the alphabet Sigma1 is empty, we have either L1 = 0 or L1 = {epsilon}. In this case, the synchronous composition technically evaluates to L_res = 0 or L_res = L2, respectively. A similar line of thought applies to the situation where Sigma2 is empty. Note. Functions in this section maintain event attributes, provided that they match for all arguments. ParallelComputes the parallel composition of two or more generators. Signature:Parallel(+In+ Generator G1, +In+ Generator G2, +Out+ Generator GRes) Parallel(+In+ GeneratorVector GVec, +Out+ Generator GRes) Parallel(+In+ Generator G1, +In+ Generator G2, +Out+ ProductCompositionMap CompMap, +Out+ Generator GRes) Detailed description:
Given two generators G1 and G2,
this function computes the parallel composition GRes = G1 || G2, with
Technically, Parallel constructs its result on the product
of the state spaces of G1 and G2, i.e. Q_res = Q1 x Q2.
Thus, to a resulting state q = (q1,q2) correspond the component states
q1 and q2.
Transitions are enabled in GRes whenever they are enabled in each component
that include the event in their respective alphabet:
There are two more variants of Parallel:
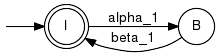
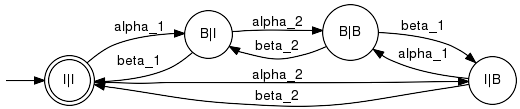
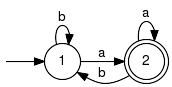
Example:Our first example composes two independent "very simple machines". Since the components do not share any events, the parallel compositions turns out as the so called shuffle product.
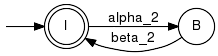
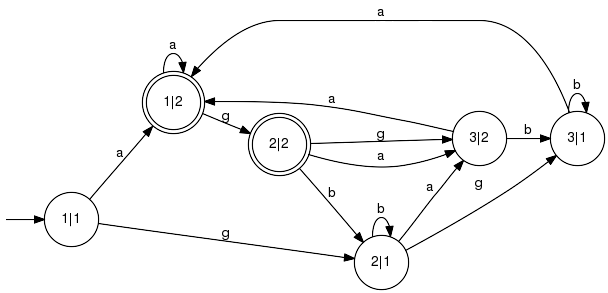
Example:In this example, the shared events are {a, b}. Component G2 does not impose any restrictions on the generated language, i.e. Pinv2(L(G2)) = Sigma*. However, G2 requires the marked language not to end with a b-event (when projected to Sigma2).
Parameter Conditions:In this implementation, only accessible states are generated. On deterministic input this functions constructs a deterministic output. The resulting generators controllability attributes are copied from the arguments. It is considered an error if the controllability flags in the arguments don't match. IsNonblockingTest a generator/ two languages for being nonblocking. Signature:IsNonblocking(+In+ Generator G, +Out+ Boolean BRes) IsNonblocking(+In+ Generator G1, +In+ Generator G2, +Out+ Boolean BRes) IsNonblocking(+In+ GeneratorVector G, +Out+ Boolean BRes) Detailed description:
An individual discrete event system modelled by a generator G
may block in the sense that it attains a state from which no marking can be reached.
Technically, G is said to be non-blocking, if
The synchronous composition of two discrete event systems modelled by
the generators G1 and G2 may block in the sense that
the one system prevents the other satisfying its acceptance condition. Formally,
two languages are non-conflicting, if
When applied to two generators, the function IsNonblocking
first performs the Parallelcomposition and then tests, whether the
resulting generator is non-blocking. Provided that the two individual generators are
non-blocking, i.e.
When a large number of generators is to be tested for conflicts, performing the overall parallel composition may not be practical. The literature [C4] addresses such situations and proposes various conflict-equivalent abstraction methods to be applied to the individual systems before composition. These methods are used when invoking IsNonblocking with the GeneratorVector argument. However, our implementation is still experimental and does not allways achieve the expected performance. Parameter Conditions:For blocking in the sense of accessible but not co-accessible states, no restrictions apply. For the language based notion of conflicts, the individual generators are must be deterministic and non-blocking for a sufficient and necessary test. ProductComputes the product composition of two genertors. Signature:Product(+In+ Generator G1, +In+ Generator G2, +Out+ Generator GRes) Product(+In+ Generator G1, +In+ Generator G2, +Out+ ProductCompositionMap CompMap, +Out+ Generator GRes) Detailed description:
Given two generators G1 and G2,
this function computes the product composition GRes = G1 x G2, with
Technically, Product constructs its result on the product
of the state spaces of G1 and G2, i.e. Q_res = Q1 x Q2.
Thus, to a resulting state q = (q1,q2) correspond the component states
q1 and q2.
Transitions are enabled in GRes whenever they are enabled in both components.
An optional output argument can be supplied to record a so called composition map, which relates the states of the result and the states of the arguments. Parameter Conditions:In this implementation, only accessible states are generated. On deterministic input this functions constructs a deterministic output. The resulting generators controllability attributes are copied from the arguments. It is considered an error if the controllability flags in the arguments don't match. libFAUDES 2.33l --- 2025.09.16 --- with "omegaaut-synthesis-observer-observability-diagnosis-hiosys-iosystem-multitasking-coordinationcontrol-timed-simulator-iodevice-priorities-luabindings-hybrid-example-pybindings" |