Generator

A generator is a finite representation of a (regular) formal language. In the context of discrete event systems, generators are used to model the dynamic behaviour in the sense that the corresponding language consists of all strings of events which the system can exhibit.

libFAUDES provides the plain Generator and the derived type System. The latter attaches controllability attributes to individual events to implement various decompositions of the alphabet from a control system perspective. Plug-ins may provide further specialized generator models.

Definition

A generator is a tuple G = (Q, Sigma, delta, Qo, Qm), with

  • the alphabet Sigma;

  • the state set Q;

  • the transition relation delta with transitions from Q x Sigma x Q;

  • the set of initial states Qo;

  • the set of marked states Qm.

The relation delta can be conveniently re-interpreted as a set-valued map on the domain Q x Sigma and extended to strings in its second argument. For o ∈ Sigma and s ∈ Sigma* let

delta(q,o)  :=  {q' ∈ Q | (q,o,q') ∈ delta}, and
delta(q,so)  :=  delta(delta(q,s),o).

The generated and marked languages L(G) and Lm(G), respectively, are defined by:

L(G)  :=  {s ∈ Sigma* | delta(Qo,s) ≠ 0}, and
Lm(G)  :=  {s ∈ Sigma* | delta(Qo,s) ∩ Qm ≠ 0 }.

When infinite length strings are to be considered, we may refer to the omega languages

B(G)  :=  {w ∈ Sigma^w | all prefixes s < w are in L(G) } ,
Bm(G)  :=  {w ∈ Sigma^w | there ex. a corresponding state sequence with inf. many states in Qm } .

The latter is refered to as Buechi acceptance condition. For deterministic generators, Bm(G) can be expressed as the limit of Lm(G):

Bm(G)  =  B(Lm(G))  :=  {w ∈ Sigma^w | infinitely many prefixes s < w are in Lm(G) } .

In particular, for deterministic generators G1 and G2 with Lm(G1) = Lm(G2) we have Bm(G1) = Bm(G2).

Example

The simple machine can

  • pick up a workpiece to process it (event alpha);

  • dump a workpiece after processing it (event beta);

  • break down while processing a workpiece (event mue);

  • be serviced after break-down (event lambda).

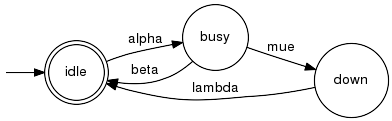
Our generator model refers to the alphabet Sigma={alpha, beta, mue, lambda} and utilises the states Q={idle, busy, down}. Transitions are given by the below graph.

Example simple machine

We decided to have idle as the only initial state, i.e. Qo={idle}. Thus, in our model we assume that the machine is initially idle and that any sequence of events to be observed therefore starts with the event alpha. This applies to both the generated and marked languages L(G) and Lm(G), respectively.

Furthermore, We have chosen Qm={idle}. In doing so, we consider only strings that run the machine into the idle state as relevant operations. The choice of Qm only affects the marked language Lm(G). The interpretation of the marked language as a model of a phenomenen is twofold: one can think of the marking to indicate a property that the phenomenon is known to satisfy, or as a condition which the environment of the phenomenon is meant to satisfy. In our example, we chose not to mark the state busy in order to express the fact that once the machine became busy, it is known that it eventually either dumps the workpiece or breaks down. For the simple machine, it is considered not posible that no more events occurs once it is in state busy. In contrast, consider the state down, which we also chose not to mark. Of course, we can imagine that no one cares about the machine once it is down and, hence, the event lambda will never occur. Here, we express the requirement that the machine needs to be serviced. A string that ends with a mue event is not considered to represent a legal operation of the machine.

Token IO

Token-IO example for a Generator that models the simple machine: 

<Generator>
% libFAUDES Generator for the simple machine
"simple machine"                   

<Alphabet>                         
alpha beta mue lambda      
</Alphabet>

<States>                           
idle busy down
</States>

<TransRel>
idle  alpha  busy
busy  beta   idle
busy  mue    down
down  lambda idle
</TransRel>

<InitStates>
idle
</InitStates>

<MarkedStates>
idle
</MarkedStates>
</Generator>

Technical Detail: Both, states and events are internaly represented as indices (non-negative integer). The correspondance between indices and symbolic names is managed transparenty by symbol tables. Valid symbolic names are strings of printable ASCII characters, excluding the double quote ", the hash # and any white space. It is not recommended to not use symbolic names that can be misinterpreted as number, i.e., consists of digits only. For events, symbolic names are mandatory, and the respective symbol table is global. For states, symbolic names are considered optional and the respective symbol table is local to the generator.

Technical Detail: Since symbolic state names are optional, states may be directly represented by an index. In order to consitently read a generator from a token stream, the convention is to index states consecutively starting from 1. For generators, which do not comply to this convetion, explicit state indices are given in the format symbol#index. In the above example, the three states are indexed 1, 2, and 3. If they were indexed 7, 8, and 9, the token format would be as follows. 

...
<States>                           
idle#7 busy#8 down#9
</States>
...

Technical Detail: The generator name is optional and defaults to generator. The alphabet and the state set are extracted from the transition relation, when not specified explicitly. Furthermore, the inner tags can be abreviated by the respective first letter, e.g. <T> for <TransRel>. Thus, the simple machine can be alternatively reresented as follows: 

<Generator>
<T>
idle  alpha  busy
busy  beta   idle
busy  mue    down
down  lambda idle
</T>
<I> idle </I>
<M> idle </M>
</Generator>

System

A System is a Generator with a controllability attribute attached to each individual event. The attribute is used to indicate controllability, observability, forcibility and whether or not the respective event is regarded a high-level event. Thus, attributes implement four disjoint union decompositions of the generator's alphabet Sigma:

  • Sigma = Sigma_c ∪ Sigma_uc,

  • Sigma = Sigma_o ∪ Sigma_uo,

  • Sigma = Sigma_f ∪ Sigma_uf and

  • Sigma = Sigma_hi ∪ Sigma_lo.

Functions, that expect Generator-typed arguments (are meant to) also accept Systems instead. When indicated by the documentation, such functions will interpret the respective attributes appropriately. Otherwise they are simply ignored. If attributes are not relevant to your application, it is recommended to stick to Generator-typed variables.

When reading or writing a System from/to a token stream, each event specified in the Alphabet section is optionally followed by a token of the form +xyz+, where each letter in xyz indicates membership in one of the above sets:

controllable +C+
uncontrollable +c+
observable +O+
unobservable +o+
forcible +F+
unforcible +f+
high-level +A+
low-level +a+
    

The default amounts to +cOfA+, i.e. o ∈ Sigma_uc ∩ Sigma_o ∩ Sigma_uf ∩ Sigma_hi.

Token-IO example for a System that models the simple machine: 

<Generator>
% libFAUDES Generator for the simple machine with controllability attributes
"simple machine"                   

<Alphabet>                         
alpha  +C+  % controllable event alpha
beta        % default, i.e. +cOfA+
mue 
lambda +CO+ % controllable and observable, same as +C+ since +O+ is default    
</Alphabet>

[ ... same as above generator example ... ]

</Generator>

The token-IO format of Systems is compatible to Generators. I.e., a System can be configured from a tokenized Generator where attributes take a default value, and, vice versa, a Generator can be configured from a System, where attributes are ignored.

libFAUDES 2.32b --- 2024.03.01 --- with "synthesis-observer-observability-diagnosis-hiosys-iosystem-multitasking-coordinationcontrol-timed-simulator-iodevice-luabindings-hybrid-example-pybindings"

>>