• libFAUDES
• Reference  
• Type Index  
• Function Index  
• Literature  
•  
• Sections
• CoreFaudes  
  • CoreFaudes
  • Introduction
  • Generators
  • Alphabets
  • Reachability
  • Boolean Operations
  • Regular Expressions
  • Synchronous Composition
  • Projection
  • StateSet Conversion
  • Elementary Types
  • Miscellaneous
  • Vector Types
• CoordinationControl  
• Diagnosis  
  • Diagnosis
  • Introduction
  • Event-Diagnosis
  • Language-Diagnosis
  • Modular Diagnosis
  • Decentralized Diagnosis
  • Application Example
• Example  
• FaultTolerantControl  
  • FaultTolerantControl
  • Introduction
  • Example
  • Fault-Accommodation
  • Reconfiguration
  • Fault-Patterns
• HioSys  
  • HioSys
  • Introduction
  • Step-By-Step
  • Synthesis Procedure
  • Liveness Properties
  • Application Example
• Hybrid  
• IoSystem  
  • IoSystem
  • Introduction
  • Properties
  • Synthesis
• Multitasking  
  • Multitasking
  • Introduction
  • Functions
  • Observer
  • Optimal Color Set
  • Reachability
  • Synthesis
• Observer  
  • Observer
  • Introduction
  • Verification
  • Synthesis
  • Example
• OmegaAut  
  • OmegaAut
  • Introduction
  • Buechi-Functions
  • Buechi-Control
• Priorities  
• Simulator  
  • Simulator
  • Introduction
  • Executor Classes
  • Hardware-In-The-Loop
  • IO-Devices
  • Simulator Interconnection
• Synthesis  
  • Synthesis
  • Introduction
  • Controllability
  • Normality
  • Completeness
  • Misc Functions
•  
• Types
• IoSystem  
•  
• Functions
• IoFreeInput  
• IoSynthesis  
• IoSynthesisClosed  
• IsInputLocallyFree  
• IsInputOmegaFree  
• IsIoSystem  
•  

I/O Systems

This plug-in addresses discrete event systems that satisfy a variation of Willems' conditions on I/O behaviours [B1]. In the context of system interconnection, the conditions imply a structural non-blocking property. In particular, one may design a controller for a plant abstraction and run it on the actual plant, without risking a blocking situation. This enables the use of discrete event systems synthesis methods to solve control problems for plants with an infinite state space, provided that a finite abstraction is available; see e.g. [B2] for a discussion of hybrid control systems from this perspective.

A detailed treatment of I/O systems from a discrete event perspective is given in Thomas Wittmann's Diploma Thesis, including how they relate to abstraction based controller design. A consise summary has been presented in [B3]. The remainder of the user reference is organized as follows:

• A Simple Example

• I/O System Definition and Properties

• I/O System Controller Synthesis

Copyright (C) 2010, Thomas Wittmann, Thomas Moor.

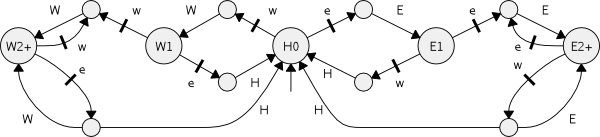
A Simple Example

Consider a vehicle on a path that can be controlled by input events e to "move to the east" and w to "move to the west", respectively. A measurement facility distinguishes a home position and issues output events H for "home", E for "east of home" and W for "west of home". The dynamics of the vehicle are modelled by the below transition system, where we use an infinite state space to represent an unbounded path.

Plant L

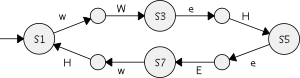
We interpret the transition system w.r.t. the infinite time axis, i.e., as an omega-language L ⊆ Sigma^w. Since state enumeration is not feasible for an infinite state set, we can not directly apply enumaration based methods from supervisory control theory. Thus, we resort to a plant abstraction with a finite state set. The abstraction L' ⊆ Sigma^w, L ⊆ L', realized by the transition system below, has been obtained by merging all states east of position E1 and all states west of position W1.

Abstraction L'

As a specification, we require the vehicle to regularly visit east and west positions. For sake of simplicity, we circumvent eventuality properties and use the more restrictive language inclusion specification E depicted below. We apply the synthesis procedure IoSynthesisClosed on the plant abstraction to obtain a controller such that K' := L'∩H ⊆ E. The procedure is essentially a wrapper for SupConComplete, i.e. output events are not disabled and any finite string can be further extended.

Specification E		Supervisor H

Clearly, the controller will also enforce the specification when applied to the actual plant L:

K :=  L∩H  ⊆  L'∩H  ⊆  E

In general, the closed loop interconnection with the actual plant may be blocking. However, for our plant at hand this is not the case. Observe that, for our plant, input events from U = {e, w} and output events from Y = {H, E, W} alternate, and that the plant in every state will accept either none or any input event. The latter property is referred to as a locally free input:

(∀ s ∈ Prefix(L) ∀ \mu, \mu' ∈ U) [ s\mu ∈ Prefix(L)    ⇒    s\mu' ∈ Prefix(L) ] ,

see also IsInputLocallyFree. Indeed, together with controllability of Prefix(H) w.r.t. to the plant abstraction Prefix(L'), the locally free input of the actual plant L forms a sufficient condition for a locally nonblocking closed loop, i.e.

Prefix(L)∩Prefix(H) is complete.

For our example, the plant also fulfills the stronger condition of a omega-free input, which implies an omega-nonblocking closed loop, i.e.

Prefix(L)∩Prefix(H) = Prefix(L∩H),

see also IsInputOmegaFree. A variation of this example that includes eventuality properties expressed via Buchi's acceptance condition is presented at IoSynthesis.

Literature

[B1] J.C. Willems: Paradigms and Puzzles in the theory of dynamical systems, IEEE Transactions on Automatic Control, vol. 36, issue 3, pp. 258--294, 1991.

[B2] T. Moor, J. Raisch: Supvervisory control of hybrid systems within a behavioural framework, Special issue on hybrid systems, System and Control Letters, vol. 38:3, pp. 157-166, 1999.

[B3] T. Moor, K. Schmidt, Th. Wittmann: Abstraction-based control for not necessarily closed behaviours, Preprints of the 18th IFAC World Congress, pp. 6988-6993, 2011.

libFAUDES 2.33h --- 2025.06.18 --- with "omegaaut-synthesis-observer-observability-diagnosis-hiosys-iosystem-multitasking-coordinationcontrol-timed-simulator-iodevice-priorities-luabindings-hybrid-example-pybindings"