• libFAUDES
• Reference  
• Type Index  
• Function Index  
• Literature  
•  
• Sections
• CoreFaudes  
  • CoreFaudes
  • Introduction
  • Generators
  • Alphabets
  • Reachability
  • Boolean Operations
  • Regular Expressions
  • Synchronous Composition
  • Projection
  • StateSet Conversion
  • Elementary Types
  • Miscellaneous
  • Vector Types
• CoordinationControl  
• Diagnosis  
  • Diagnosis
  • Introduction
  • Event-Diagnosis
  • Language-Diagnosis
  • Modular Diagnosis
  • Decentralized Diagnosis
  • Application Example
• Example  
• FaultTolerantControl  
  • FaultTolerantControl
  • Introduction
  • Example
  • Fault-Accommodation
  • Reconfiguration
  • Fault-Patterns
• HioSys  
  • HioSys
  • Introduction
  • Step-By-Step
  • Synthesis Procedure
  • Liveness Properties
  • Application Example
• Hybrid  
• IoSystem  
  • IoSystem
  • Introduction
  • Properties
  • Synthesis
• Multitasking  
  • Multitasking
  • Introduction
  • Functions
  • Observer
  • Optimal Color Set
  • Reachability
  • Synthesis
• Observer  
  • Observer
  • Introduction
  • Verification
  • Synthesis
  • Example
• Simulator  
  • Simulator
  • Introduction
  • Executor Classes
  • Hardware-In-The-Loop
  • IO-Devices
  • Simulator Interconnection
• Synthesis  
  • Synthesis
  • Introduction
  • Controllability
  • Normality
  • Omega-Controllability
  • Misc Functions
•  
• Types
• EventRelabelMap  
•  
• Functions
• InsertRelabeledEvents  
• IsLocallyControlConsistent  
• IsMsaObserver  
• IsMutuallyControllable  
• IsNaturalObserver  
• IsOutputControlConsistent  
• MsaObserver  
• MsaObserverLcc  
• NaturalObserverExtension  
• NaturalObserverLcc  
• NaturalObserverRelabeling  
•  

Observers

This plug-in implements algorithms that support the hierarchical supervisor synthesis with the aim of reducing the computational synthesis effort for large-scale discrete event systems. In this regard, the plug-in employs different variants of the observer property for natural projections introduced in [O1] for the nonblocking hierarchical supervisory control. Both verification algorithms for the observer property and algorithms for the computation of natural projections that possess the observer property are provided. In addition, the plug-in integrates the local control consistency (LCC) condition [O2],[O5] for the maximally permissive hierarchical supervisory control.

We provide an introduction to this plug-in by means of the below basic hierarchical supervisor design flow. Advanced ussage is illustrated by a large-scale laboratory setup [O4].

The remainder of this section is organised as follows:

• Introduction (see Example below)

• Verification of Observer Properties

• Synthesis of Observers

• Large-Scale Example

Copyright (c) 2006, Bernd Opitz
Copyright (c) 2008, Christian Breindl, Klaus Schmidt.

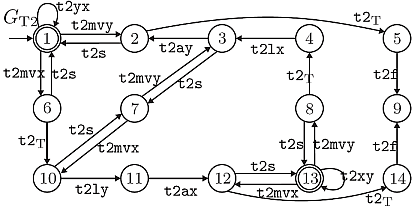
Local Control and Hierarchial Abstraction -- Example

We illustrate the hierarchical synthesis by the rotary table component T2 of a larger manufacturing system model in the figure below. We first present a detailed automata model G_T2 of the rotary table T2. The rotary table has two defined positions (x-position and y-position) that are indicated by switch-keys which are pressed whenever the respective position is taken. In our model, the sensor events t2ax/t2lx occur when T2 arrives at/leaves the x-position and t2ay/t2ly occur when T2 arrives at/leaves the y-position. Furthermore, T2 can rotate as shown by the arrows in the figure, whereby the motion is triggered by the actuator events t2mvx ("move to the x-position") and t2mvy ("move to the y-position"), and T2 stops when t2s occurs. Moreover, the additional event t_T2 represents the passage of time, t2f indicates the system failure that happens if the rotary table overruns one of the switch-keys, and the logical events t2xy and t2yx are supposed to initiate the motion of T2. Considering the event attributes, all sensor events and t2f are uncontrollable, all actuator events, logical events and t_T2 are controllable. Finally, it is assumed that T2 initially holds the y-position, and the marking captures that is is always desired to reach one of the defined positions.

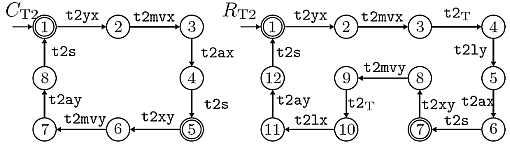
We now compute a local supervisor for the rotary table T2. The specification C_T2 is shown in the figure below. It states that T2 has to move between its defined positions without stopping or changing the direction of motion. Then, R_T2 in the subsequent figure represents the nonblocking and maximally permissive closed-loop that is computed by invoking SupConNB(G_T2,C_T2,R_T2).

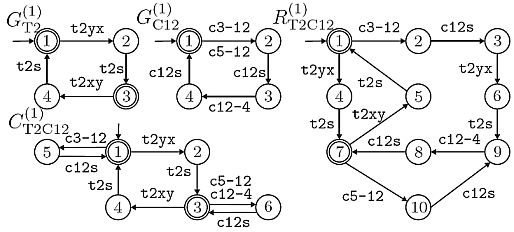
The operation of the rotary table T2 is directly dependend on the operation of the conveyor belt CB12 that is mounted on T2. That is, a supervisor for the joint behavior of T2 and CB12 has to be computed. In particular, it is desired that T2 does not move while CB12 is transporting workpieces and T2 should always have the correct (x or y)-position for the transport of workpieces by CB12. Noting that the relevant information of T2 is encoded in the occurrence of the events t2yx,t2xy and t2s, it is sufficient to use an abstraction of the behavior of R_T2 to the alphabet \hatSigma_T2 = {t2yx,t2xy,ts} for the supervisor synthesis. Natural projections that possess the natural observer or the marked string accepting observer condition are suitable for this purpose. For T2, we verify that both conditions are fulfilled by using the observer plug-in functions IsNaturalObserver(R_T2,\hatSigma_T2) and IsMsaObserver(R_T2,\hatSigma_T2), respectively. (Note that an appropriate extension of \hatSigma_T2 can be computed by NaturalObserverExtension(R_T2,\hatSigma_T2) and MsaObserver(R_T2,\hatSigma_T2) if the respective conditions are violated by \hatSigma_T2). In addition, it can be verified by the function IsLocallyControlConsistent(R_T2,\hatSigma_T2) that the natural projection of R_T2 to the alphabet Sigma_T2 is locally control consistent as a sufficient condition for maximally permissive control.

After the successful verification, we abstract the obtained closed-loop R_T2. We use the natural projection p_T2:Sigma_T2*→\hatSigma_T2* from the original alphabet of G_T2 to the abstraction alphabet \hatSigma_T2 =  {rtyx, rtxy, rs}, resulting in G_T2^(1) in the figure below.

In addition to the abstracted model G_T2^(1), the above figure shows an abstraction G_CB12^(1) of the conveyor belt CB12 that is already locally controlled by a supervisor R_CB12. Here, the events c3-12,c5-12,c12-4 symbolize the transport of a workpiece to/from neighboring components while the event c12s occurs when CB12 stops. Using the parallel composition G_T2^(1)||G_CB12^(1), it is now possible to compute a supervisor for the specified joint action of T2 and CB12 as described above and formalized by the automaton C_T2CB12^(1). The required operation is SupConNB(G_T2^(1)||G_CB12^(1),C_T2CB12^(1),R_T2CB12^(1)). Together, the synthesis for T2 and CB12 yields two local supervisors with 12 and 17 states, respectively, and one coordinating high-level supervisor with 10 states, whereby the largest automaton in the computation has 47 states. In contrast, a monolithic supervisor has 73 states and requires the enumeration of an automaton with 752 states. As an extension of this preliminary example, please consult the hierarchical supervisor synthesis for a large-scale laboratory setup.

Literature

[O1] K.C. Wong and W.M. Wonham: On the computation of observers in discrete event systems, Discrete Event Dynamic Systems, vol. 14, no. 1, pp. 55-107, 2004.

[O2] K. Schmidt and C. Breindl: On maximal permissiveness of hierarchical and modular supervisory control approaches for Discrete Event Systems, Workshop on Discrete Event Systems, 2008.

[O3] K. Schmidt, Th. Moor, S. Perk: Nonblocking hierarchical control of decentralized discrete event systems, IEEE Transactions on Automatic Control, 53(10):2252-2265, 2008.

[O4] Th. Moor, K. Schmidt, S. Perk: Applied Supervisory Control for a Flexible Manufacturing System, Workshop on Discrete Event Systems, 2010.

[O5] K. Schmidt, Ch. Breindl: Maximally Permissive Hierarchical Control of Decentralized Discrete Event Systems, available at IEEE Transactions on Automatic Control,56(5), 2011.

[O6] L. Feng and W. Wonham: On the computation of natural observers in discrete-event systems, available at Discrete Event Dynamic Systems: Theory and Applications, 20(1):63-102, 2010.

libFAUDES 2.32b --- 2024.03.01 --- with "synthesis-observer-observability-diagnosis-hiosys-iosystem-multitasking-coordinationcontrol-timed-simulator-iodevice-luabindings-hybrid-example-pybindings"