Hierarchical I/O Systems (HioSys)

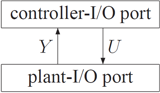
Introduction to inputs and outputs

A system description S = (L,Sigma) with a regular language L over the alphabet Sigma is given I/O structure by providing it with a plant-I/O port or a controller-I/O port.

Plant-I/O port

A plant-I/O port is designed to be an interface of the plant to an operator or controller for manipulation of the plant behaviour.

Definition: A plant-I/O port of a system (L,Sigma) is a tuple (U,Y) of input and output events, with

• Sigma = W ∪ U ∪ Y, U ≠ 0 ≠ Y;

• L ⊆ Closure((YU+W)*);

• (∀ s ∈ Sigma* Y, \mu ∈ U)[s ∈ L ⇒ s\mu ∈ L].

The first bullet point separates input events U from output events Y and remaining events W. The second bullet point requires alternation of input and output events aiming at a dependence between cause and effect. Remaining dynamics (e.g. dynamics performed on another I/O port) is captured by W*. The third item requires all input events to be accepted after an output event ("free input U").

The notion of input- and output-events does not match with the classical notion of controllable and uncontrollable events (see controllability). A controllable event, for example, may at the same time be input of a plant model and output of a controller.

Controller-I/O port

A controller-I/O port (U,Y) is designed to be an interface of an operator or controller to the plant. It is a complement of the plant-I/O port in the sense that it accepts any Y-event as an input issued by a plant-I/O port. In return, it can provide an event out of U; see Definition. A controller-I/O port can be connected to a plant-I/O port to form a feedback structure.

Simple feedback structure of plant- and controller-I/O port

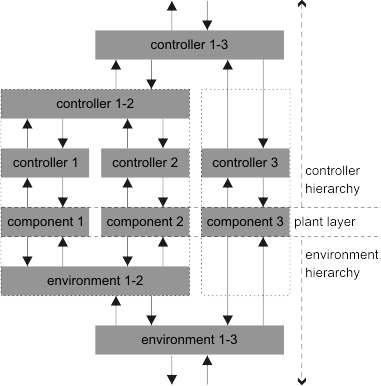
This simple feedback structure already establishes a continuous chain of cause and effect: if, apart from each other, a plant- and a controller-I/O port can continuously produce events, then the same holds for the feedback loop of both entities. The above definitions of a plant- and a controller-I/O port already allow for non-hierarchical controller-synthesis, where controllability results as a consequence of the I/O-structure, see the below example. Plant- and controller-I/O port are used to define the entities HioPlant, HioController and HioEnvironment that form an I/O-based hierarchy as in the above picture.

Example

The example shall illustrate and motivate the particular I/O structure for discrete event models that is used in our approach. Hence, it does not serve as terms of use for the HioSys-PlugIn.

We consider the same two very simple machines M1 and M2 as in the Synthesis-PlugIn.

Plant Model

Each machine can process one workpiece at a time. Per machine Mi (i=1,2), the conventional model distinguishes the two events alpha_i and beta_i to indicate the beginning and the end of the machine processing a workpiece.

For an I/O-based plant description, we introduce the plant-I/O port (Ui,Yi) and assign alpha_i to the set Ui, as the beginning of the process is initiated by an operator or controller, i.e. poses an input to the system Mi. The end of the process beta_i is induced by the machine itself and thus belongs to the set of Yi-events. For situations, where the machine is not processing a workpiece or the operator (or controller) does not start a process, we supplement Yi and Ui by the events idle_i ("ready for next workpiece") and no_op_i ("no operation"), respectively. The behaviour of the two machines is modeled as a plant-I/O port (U1,Y1) and (U2,Y2) by the below Generators G1 and G2, respectively. The states I and B refer to the machine being idle or busy, while the states _U and _Y indicate if input- or output-events, respectively, are enabled next.

The overall plant model is constructed as the I/O-shuffle product of both components, which is computed on the basis of the function Parallel with additional restriction on the I/O structure of the result that, in this case, evaluates to the structure of a plant-I/O port (U,Y) := (U1\∪ U2, Y1 ∪ Y2). Hence, the I/O shuffle of both components accepts all input events U1∪U2 after an output event. Yet, U2-events after an Y1-event or U1-events after an Y2-event are considered erroneous ("answer to wrong component") and lead to the error states 2 and 3.

(The I/O shuffle used for this non-hierarchical example is a special and unpublished variant of the function HioShuffle that is designed for the general hierarchical case.)

Plant Component G1 Plant Component G2

I/O shuffle of G1 and G2

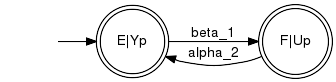
Specification

Analogously to the Supervisory Control Theory (see Synthesis), the specification models the set of all acceptable strings. In our scenario, the two machines shall be arranged with a buffer to implement a two-stage production process. Each workpiece must first be processed by M1, then placed in the buffer B, and finally processed by M2. The buffer capacity is restricted to one workpiece. While by our plant model both machines act independently, the buffer imposes a condition regarding the interaction of both machines. We model the buffer as our specification, where the event beta_1 fills the buffer and alpha_2 empties the buffer. By convention, the remaining events may occur at any time.

Specification

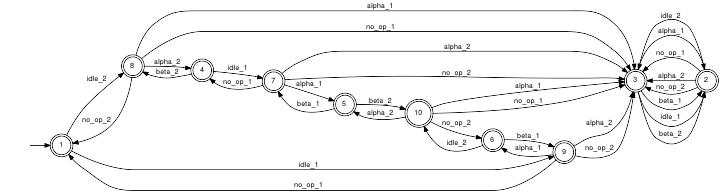
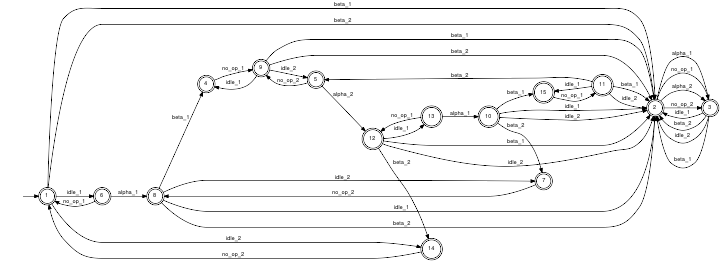
Controller

In the non-hierarchical case, the controller is directly computed as controller-I/O port that enforces the specification on the plant-I/O port while strictly accepting all plant output events Y. Unexpected Y-events, i.e. those that cannot occur at the current state of the plant-I/O port, lead to error states (states 2 and 3) of the controller-I/O port. An example for an unexpected Y-event is the occurrence of beta_2 in the initial state of the controller.

Controller (Synthesized by an unpublished non-hierarchical variant of the function HioSynth.)

Note that, if the machine M2 is still busy and the buffer is full (state 15), the controller will prevent that machine M1 takes up a workpiece by allowing for no_op1 only. If the controller did not prevent M1 from taking up a workpiece, it could happen, that M1 finishes processing before M2 and, hence, a buffer overflow would occur. The closed loop behaviour is given by the parallel composition (Parallel) of the controller and the above I/O shuffle of G1 and G2. By the function Project, we can remove all events but the physical events alpha_i and beta_i to obtain the physical closed loop behaviour, which proves to be identical to the supervisor that is achieved by application of the Supervisory Control Theory (see Synthesis).

Learn more about:

• Introduction to inputs and outputs

• Hierarchical design - step by step

• Application example

• Synthesis procedure

• I/O-based liveness

Literature

[H1] S. Perk, T. Moor and K. Schmidt: Hierarchical Discrete Event Systems with Inputs and Outputs, Proceedings. 8th International Workshop on Discrete Event Systems (WODES06) , 2006.

[H2] S. Perk, T. Moor and K. Schmidt: Controller Synthesis for an I/O-Based Hierarchical System Architecture, Proceedings. 9th International Workshop on Discrete Event Systems (WODES08), 2008.

[H3] J.C. Willems: Paradigms and puzzles in the theory of dynamic systems, IEEE Transactions on Automatic Control, vol. 36, issue 3, pp. 258--294, 1991.

[H4] T. Moor, J. Raisch and J.M. Davoren: Admissibility criteria for a hierarchical design of hybrid control systems, Proceedings. IFAC Conference on the Analysis and Design of Hybrid Systems (ADHS03), 2003.

[H5] T. Jéron, H. Marchand, V. Rusu and V. Tschaen: Ensuring the conformance of reactive discrete-event systems using supervisory control, Proceedings. 42nd IEEE Conference on Decision and Control (CDC03), 2003.

top of page

libFAUDES 2.32b --- 2024.03.01 --- with "synthesis-observer-observability-diagnosis-hiosys-iosystem-multitasking-coordinationcontrol-timed-simulator-iodevice-luabindings-hybrid-example-pybindings"