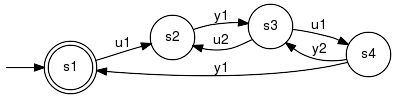
I/O Systems Definition and Properties

IoSystem

The IoSystem class implements a generator G with specialized event attributes to represent the overall alphabet as a disjoint union of input events and output events; i.e., Sigma = U∪Y. The intention is to impose conditions on the transition relation that justify the interpretation of inputs and outputs from a behavioural perspective: according to [B1], I/O systems have a free input and the output does not anticipate the input.

Both properties are originally stated in terms of behaviours, i.e., sets of signals on some infinite time axis, typically the reals or the integers. For the discrete event setting within libFAUDES, we focus our attention to omega-languages where input events and output events are required to alternate. Thus, an object of type IoSystem is interpreted as the omega language L = Bm(G) and we require L ⊆ (UY)^w. The latter can be verified by IsIoSystem; for further properties related to inputs and outputs, see IsInputLocallyFree and IsInputOmegaFree.

Example:

Simple I/O system with U = {u1, u2} and Y = {y1, y2}.

Token IO

The token format is identical with the standard Generator, except for the event attribute +I+ for input events and +O+ for output events. 

<Generator>
"IOSystem"           

<Alphabet>
"u1"    +I+     "u2"    +I+
"y1"    +O+     "y2"    +O+
</Alphabet>

<States>
"s1"  "s2" "s3"	"s4"
</States>

<TransRel>
"s1"	"u1"	"s2"

"s2"	"y1"	"s3"

"s3"	"u1"	"s4"
"s3"	"u2"	"s2"

"s4"	"y1"	"s1"
"s4"	"y2"	"s3"
</TransRel>

<InitStates>   
"s1" 
</InitStates>

<MarkedStates> 
"s1" 
</MarkedStates>

</Generator>

IsIoSystem

Test for basic I/O properties.

Signature:

IsIoSystem(+InOut+ IoSystem GArg, +Out+ Boolean BRes)

Detailed description:

The function IsIoSystem tests whether the event attributes are consistent with the transition system. It returns true if

  • the alphabet is the disjoint union of input and output events; and if

  • either L(G) ⊆ (UY)* or L(G) ⊆ (YU)*; and if

  • Lm(G) is complete.

This implementation also sets state attributes to indicate whether a state has outgoing input events or outgoing output events. When the test fails, conflicting states get an error attribute attached.

Example:

All examples in this reference satisfy the above conditions, including the generator given at IoSystem.

Parameter Conditions:

There are no conditions on the arguments.

IsInputLocallyFree

Test for the input to be locally free.

Signature:

IsInputLocallyFree(+InOut+ IoSystem GArg, +Out+ Boolean BRes)

Detailed description:

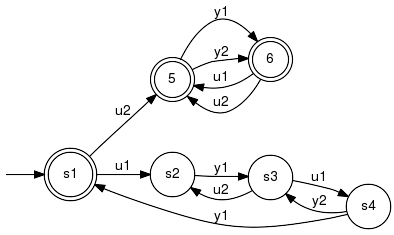
The function IsInputLocallyFree tests if whenever some input event can be applied then any other input symbol can be applied, too. Technically, the I/O system (G, U, Y) exhibits a locally free input U if

(∀ s ∈ Prefix(L) ∀ \mu, \mu' ∈ U) [ s\mu ∈ Prefix(L)    ⇒    s\mu' ∈ Prefix(L) ] ,

where L = B(G). Indeed, for omega-closed languages L ⊆ (YU)^w, the above property can be verified to be equivalent to a free input and a non-anticipating output in the behavioural sense [B1].

The current implementation iterates over all states and inspects outgoing transitions. If the generator is accessible, the test is equivalent to the above definition. Otherwise it is sufficient. When the test fails, conflicting states get an error attribute attached.

Example:

The I/O system given at IoSystem does not possess a free input U, since input event u1 is enabled in state s1 while u2 is disabled.

The plant L as well as the abstraction L' in the vehicle example both exhibit a locally free input.

Parameter Conditions:

There are no conditions on the arguments.

IsInputOmegaFree

Test for the input to be free in the behavioral sense.

Signature:

IsInputOmegaFree(+InOut+ IoSystem GArg, +Out+ Boolean BRes)

Detailed description:

An I/O system exhibits an omega-free input U, if the input is locally free (see IsInputLocallyFree) and if the system can always control the execution sequence to reach a marked state by choosing appropriate output events in a causal fasion.

Technically, the I/O system (L, U, Y) exhibits an omega-free input U if U is a locally free input of L = Bm(G) and if for each s ∈ Prefix(L) there exists a V ⊆ L, s ∈ Prefix(V), such that

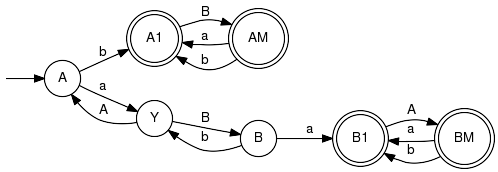
  • Prefix(V) is controllable w.r.t. (Prefix(L),U), and

  • V is relatively omega-closed w.r.t. L.

Note that the above condition is closely related to the notion of omega-controllability where U (!!) are regarded the uncontrollable events. Note also that for omega-closed I/O systems, the properties of a locally free input and an omega-free input are equivalent.

Example:

The plant L as well as the abstraction L' in the vehicle example both exhibit an omega-free input.

The below I/O system satisfies the original behavioural conditions states in [B1], including a non-anticipating output, where U = {a, b}, Y = {A, B}. It does, however, not possess an omega-free input U.

Parameter Conditions:

The current implementation assumes the specified IoSystem to be deterministic.

IoFreeInput

Inserts transitions to obtain a free input.

Signature:

IoFreeInput(+InOut+ IoSystem GArg)

IoFreeInput(+InOut+ Generator GArg, +InOut+ EventSet SigU)

Detailed description:

When the specified generator fails to exhibit a locally free input, this procedure introduces a pair of dummy states with arbitrary behaviour and adds transitions in order to formally achieve a locally free input. This function is meant to ease manual editing of I/O systems.

Example:

Applying FreeInput to the example given at IoSystem, one obtaines

Note that the resulting system does not possess an omega-free input, since once in state s2, the execution can not be controlled by choosing output events to attain a marked state.

Parameter Conditions:

Determinism of the specified IoSystem is maintained.

libFAUDES 2.32f --- 2024.12.22 --- with "synthesis-observer-observability-diagnosis-hiosys-iosystem-multitasking-coordinationcontrol-timed-simulator-iodevice-luabindings-hybrid-example-pybindings"

>>