| |
|
||||||
|
|
|||||||
|
Misc Synthesis Related FunctionsFunctions in this section are either still experimental or simply did not fit into another section. SupTconComputes the supremal controllable sublanguage w.r.t. forcible/preemptyble events. Signature:SupTcon(+In+ System GPlant, +In+ Generator GSpec, +Out+ Generator GSupervisor) SupTcon(+In+ Generator GPlant, +In+ EventSet AContr, +In+ EventSet AForcib, +In+ EventSet APreemp, +In+ Generator GSpec, +Out+ Generator GSupervisor) Detailed description:The temporal concepts of forcibility and preemptability are most conveniently studied in the context of timed discrete-event systems (TDES). However, the current version of libFAUDES does not provide conversion routines from timed activity graphs to timed discrete-event systems. For the time being, there is only a pragmatic implementation for the synthesis of the following notion of controllability. Consider two languages L and K over a common alphabet Sigma, a set of uncontrollable events Sigma_uc ⊆ Sigma, a set of forcible events Sigma_f ⊆ Sigma, and a set of preemptable events Sigma_p ⊆ Sigma_uc with Sigma_f ∩ Sigma_p = 0.
Then K is said to be controllable w.r.t. (L,Sigma_uc,Sigma_f,Sigma_p) iff for all s ∈ Closure(K)
For Sigma_p = {tick} ⊆ Sigma_uc, the above notion of controllability should match the common setting of controllability for TDES. The function SupTcon seeks to compute the supremal controllable subset of K∩L with K = Lm(GCand) and L = Lm(GPlant), referring to the above deefinition. The current implementation inspects the transitions in the product composition GPlant x GCand and removes those which conflict with the definition until a trim generator is obtained. Parameter Conditions:This implementation requires the alphabets of plant and specification to match. Furthermore, both generators must be deterministic. Effectively, the specification is intersected with the plant language. [Experimental!] The implemenation needs more testing -- please report back on unexpected behaiour. [Note] We should introduce a preemptable flag in the System data-type for more a convenient user interface. IsStdSynthesisConsistentTest consistency of an abstraction w.r.t. standard controller synthesis. Signature:IsStdSynthesisConsistent(+In+ System GPlant, +In+ Generator GPlant0, +Out+ Boolean BRes) IsStdSynthesisConsistent(+In+ Generator GPlant, +In+ EventSet AContr, +In+ Generator GPlant0, +Out+ Boolean BRes) Detailed description:Given a plant and an abstraction thereof, we ask the question whether any controller designed for the abstraction leads to a well-posed closed loop when applied to the actual plant. Answers to this question not only depend on the abstractions under consideration, but also on the detailed set of requirements imposed on the closed loop: on the abstraction level, closed-loop propeties are satisfied by design, while for the actual closed loop they need to be implied by the abstraction at hand. For the natural projection as an abstraction, the corresponding inverse projection for controller implementation, and the common closed-loop requirements of controllability and non-conflictingness, the above question has been discussed in [S7]. In particular, it is demonstrated by example that the well-studied natural observer property is a sufficient but restrictive condition for an affirmative answer. The below test implements (a variation of) the sufficient and necessary criterion developed in [S7]. Given a plant behaviour L = Lm(GPlant), consider an abstraction Lo = Lm(GPlant0) obtained by natural projection, i.e., Lo = Po(L). Then, the function IsStdSynthesisConsistent returns true if and only if for any controllable and relatively closed sublanguage Ko ⊆ Lo, the language Pinvo(Ko)∩L is a controllable and relatively closed sublanguage of the actual plant L. Acknowledgement: the initial version of this functions was implemented by Matthias Leinfelder in course of his bachelor thesis. Example:
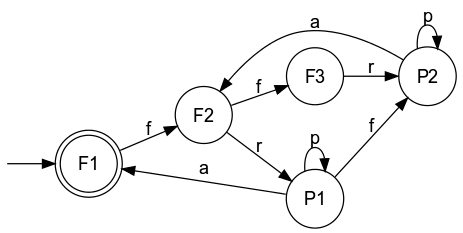
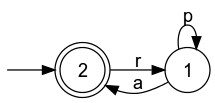
The below example is taken from [S7] and refers to the
alphabets Sigma_o = {
The function IsStdSynthesisConsistent returns true, to indicate that the abstraction is suitable for the common synthesis approach. Note, though, the projection fails to be a natural observer. Parameter Conditions:Both generators must be deterministic. The abstraction GPlant0 must have been obtained from the plant GPlant by natural projection; this prerequisit is not tested (!). The set of controllable events must be a subset of the abstraction alphabet specified by GPlant0. SupReduceCompute a reduced supervisor. Detailed description:Given a plant and a supervisor, this function seeks to compute an alternative supervisor with a reduced state count, while maintaining the closed-loop behaviour. SupReduce returns "true" to indicate success.
The problem of supervisor reduction was first discussed in [S3].
When plant and supervisor are given as gerenators G and S
over a common alphabet Sigma,
one seeks for a state minimal supervisor S_red
and an alphabet Sigma_red such that
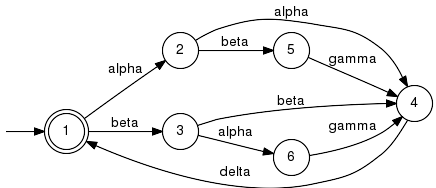
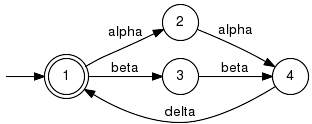
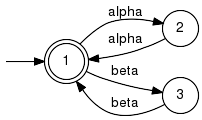
Example:The below example is taken from [S3]. We have
The reduced supervisor has only three states and a reduced alphabet Sigma = {alpha,beta}. In this example, it turns out that the supervisor GSup does not need to take any action in states 1 and 4. Hence, these two states can be merged to state 1 in the reduced supervisor GSupRed. It also has to be noted that the supervisor does not need to take any action if the events gamma or delta occur. Hence, these events do not appear in the alphabet of GSupRed. Parameter Conditions:This implementation requires the alphabets of the given plant and supervisor to match. Furthermore, both generators must be deterministic. libFAUDES 2.33l --- 2025.09.16 --- with "omegaaut-synthesis-observer-observability-diagnosis-hiosys-iosystem-multitasking-coordinationcontrol-timed-simulator-iodevice-priorities-luabindings-hybrid-example-pybindings" |