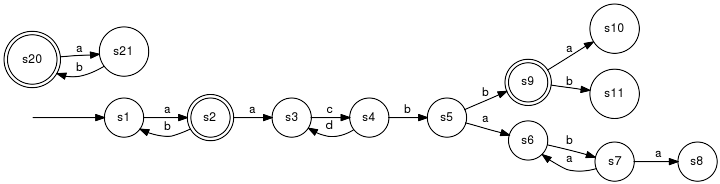
Reachability Tests/Conversion

IsAccessible

Tests a generator for accessibility.

Detailed description:

A generator is accessible, if every state can be accessed from some initial state via a sequence of transitions, i.e.:

( ∀ q ∈ Q ) ( ∃ s ∈ Sigma* ) [ delta(Qo,s) ≠ 0 ].

This function returns "true" if G is accessible. Else it returns "false".

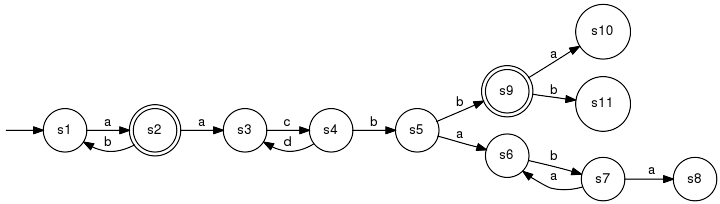
The example generator fails to be accessible since the states s20 and s21 can not be reached from the initial state.

Accessible

Delete non-accessible states and transitions.

Detailed description:

Convert a given generator G to an accessible generator by removing states that are not accessible. Non of the languages L(G), Lm(G), B(G) and Bm(G) are affected.

When applied on the above example, Accessible returns the result:

IsCoaccessible

Tests a generator for coaccessibility.

Detailed description:

A generator is co-accessible, if every state is connected with some marked state via a sequence of transitions, i.e.

( ∀ q ∈ Q ) ( ∃ s ∈ Sigma* ) [ delta(q,s)∩Qm ≠ 0 ].

This function returns "true" if G is co-accessible. Else it returns "false".

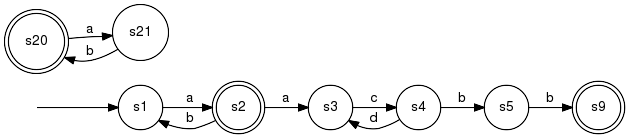
The example generator fails to be co-accessible since no marked state can be reached from either s6, s7, s8, s10 and s11.

Coaccessible

Delete non-coaccessible states and transitions.

Detailed description:

Convert a given generator G to a co-accessible generator by removing states that are not co-accessible. The languages Lm(G) and Bm(G) are not affected.

When applied on the above example, Coaccessible returns the result:

IsComplete

Test completeness of a generator.

Detailed description:

A generator G is complete if it has no terminal states, i.e., if all states have at least one transition to a successor state:

( ∀ q ∈ Q ) ( ∃ o ∈ Sigma ) [ delta(q,o) ≠ 0 ].

This function returns "true" if G is complete. Else it returns "false".

Completeness of G implies completeness of the generated language L(G), i.e.

( ∀ s ∈ L ) ( ∃ r ∈ L )  [ s < r ] .

If the generator is accessible, completeness of G is equivalent to completeness of L(G). If the generator is trim, completeness of G is equivalent to completeness of the marked language Lm(G).

The example generator fails to be complete since the states s8, s10 and s11 have no successor.

For a generalisation of the completeness property, consider an alphabet Sigma_o ⊆ Sigma. Then, a generator G is said to be Sigma_o-complete if, starting from any state, there exists a sequence of transitions ending with an event from Sigma_o, i.e.

( ∀ q ∈ Q ) ( ∃ s ∈ Sigma*Sigma_o ) [ delta(q,s) ≠ 0 ].

When invoking IsComplete with an alphabet specified, it tests for Sigma_o-completeness. The current implementation first identifies target states in which an event from Sigma_o is enabled and then performs a backward reachability analysis to obtain the set of good states that can reach the target. If all states are good, the test is passed.

Complete

Delete states that evolve into a terminal state.

Detailed description:

Convert a given generator G to a complete generator by iteratively removing terminal states until a fixpoint is reached. into a state that has no successor state; see also IsComplete. The languages B(G) and Bm(G) are not affected. The language generated by the result GRes is the supremal complete sublanguage K↑ of L(G):

K↑ = sup{ K ⊆ L(G) | K is complete} .

When applied on the above example, Complete returns the result:

When invoking Complete with an alphabet Sigma_o ⊆ Sigma specified, it refers to the more general notion of Sigma_o-completeness; see also IsComplete. Here, the implementation first identifies target states which have an event from Sigma_o enabled, and then performs a backward reachability analysis to obtain good states that can reach the target. An outer iteration restricts the target states by requiring a transition to good states until a fixpoint is reached. Finally, the generator is restricted to the set of good states. The language generated by the result GRes is the supremal Sigma_o-complete sublanguage K↑ of L(G):

K↑ = sup{ K ⊆ L(G) | K is Sigma_o-complete} .

When applied to the example with Sigma_o = {b}, Complete returns the result as above. When applied with Sigma_o = {c}, one obtains:

IsTrim

Tests a generator for trimness.

Detailed description:

A generator G is trim if it is both accessible and co-accessible, i.e. if all states contribute to the marked language Lm(G). This function returns "true" if G is trim. Else it returns "false".

The example generator fails to be trim since it is neither accessible nor co-accessible.

Trim

Delete non-coaccessible and non-accessible states and transitions.

Detailed description:

Convert a given generator G to a trim generator by removing states that are not accessible or not co-accessible. The languages Lm(G) and Bm(G) are not affected.

When applied on the above example, Trim returns the result:

IsOmegaTrim

Tests a generator for omega trimness.

Detailed description:

A generator G is omega-trim if it is accessible, co-accessible, and complete; i.e. if all states contribute to the omega language Bm(G). This function returns "true" if G is omega-trim. Else it returns "false".

The example generator fails to be trim since it is neither accessible nor co-accessible nor complete. Clearly, any state that is not accessible or not co-accessibe does contribute to Bm(G), neither does a state that is guaranteed to evolve into a state with no successor. Note, however, the states s3 and s4 do not fall into any of the latter cathegories but still don't conribute to Bm(G). This is because s3 and s4 can evolve into a marked state and they can be extended infinitely, but they can not be extended infinitely while passing marked states infinitely often.

OmegaTrim

Delete states to achieve omega-trimness.

Detailed description:

Convert a given generator G to an omega-trim generator by repeatedly removing states that are not accessible, not co-accessible, or have no successor state. The language Bm(G) is not affected.

When applied on the above example, OmegaTrim returns the result: