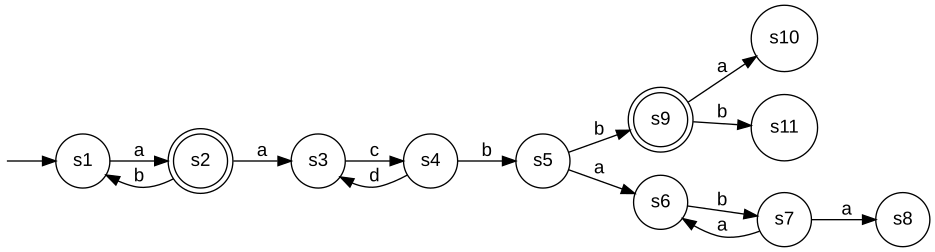
Functions on Buechi Automata

IsBuechiTrim

Tests a Buechi automaton for trimness.

Detailed description:

A Buechi automaton G is trim if it is accessible, co-accessible, and complete; i.e. if all states contribute to the accepted language Bm(G). This function returns "true" if G is omega-trim. Else it returns "false".

Example:

G

The example generator fails to be trim since it is co-accessible nor complete. Clearly, any state that is not does contribute to Bm(G), neither does a state that is guaranteed to evolve into a state with no successor. Note, however, the states s3 and s4 do not fall into any of the latter cathegories but still don't conribute to Bm(G). This is because s3 and s4 can evolve into a marked state and they can be extended infinitely, but they can not be extended infinitely while passing marked states infinitely often.

BuechiTrim

Delete states to achieve omega-trimness.

Detailed description:

Trim a given Buechi automaton G by repeatedly removing states that are not accessible, not co-accessible, or have no successor state. The accepted language Bm(G) is not affected.

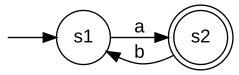
When applied on the above example, BuechiTrim returns the result:

IsBuechiClosed

Tests a language for being topolicigally closed.

Detailed description:

A omega-language L ⊆ Sigma^w is topologically closed if any strictly increasing sequence of prefixes from L converges to an omega-string in L, i.e. if

L = B(Prefix(L)),

where Prefix(L) ⊆ Sigma* denotes the set of all finite prefixes from L and B(.) is the adherence operator.

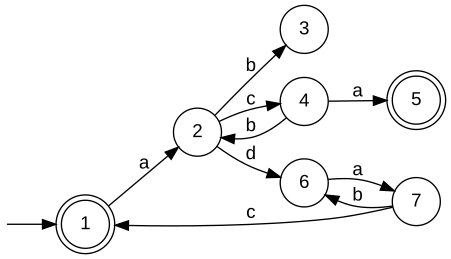
The function IsBuechiClosed tests for the specified Buechi automaton G whether Bm(G) is topologically closed. The implementation first computes the omega-trim state set. If within this set there exists an SCC with no marked states the function returns false. Else it returns true.

Example:

G

The language Bm(G) realized by the above Buechi automaton is not topolgically closed. The states 6 and 7 constitute an SCC when restricting G to the buechi-trim state set {1,2,4,6,7}. Thus, the limit of the sequence a d (a b)^i is in B(Prefix(L)) but not in B(L). The function IsBuechiClosed returns false.

Parameter Conditions:

The argument must be deterministic.

BuechiClosure

Realise topological closure for given language.

Detailed description:

For any omega-language L ⊆ Sigma^w there exists a smallest omega-closed superset, the so-called topological closure of L:

Closure(L) = B(Prefix(L)) ⊆ Sigma^w,

where Prefix(H) ⊆ Sigma* denotes the set of all finite prefixes from H and B(.) is the limit operator ; see also IsBuechiClosed.

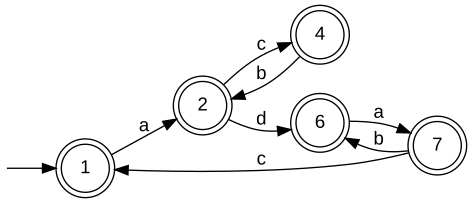
The function BuechiClosure computes a realisation of the the topological closure for the specified omega language Bm(GArg). It first invokes BuechiTrim and then markes all states. Thus, Closure(Bm(GArg)) = B(GRes) = Bm(GRes) and Prefix(Bm(GArg)) = L(GRes) = Lm(GRes).

Example:

G GRes

IsBuechiRelativelyClosed

Test for relative closedness of Buechi accepted language

Detailed description:

An omega-language K is relatively closed w.r.t. the omega-language L, if K can be recovered from its closure and L. Formally:

K = Closure(K) ∩ L .

Note that, the closure operator refers to the so called topological closure; see also BuechiClosure.

This function tests, whether

Bm(GCand) = B(GCand) ∩ Bm(GPlant)

by performing the product composition of the two generators in order to verify the following three conditions:

• L(GCand) ⊆ L(GPlant);

• no SCC of GPlant x GCand without GCand-marking contains a state with GPlant-marking; and

• no SCC of GPlant x GCand without GPlant-marking contains a state with GCond-marking.

The function returns "true" if all conditions are satisfied.

Example:

Consider the A-B-machine in the variant in which B exhausts the machine with the specification that persistently requires any sucessful operation; see Omega Synthesiss Example. Then the product will generate strings b c (b d)^*. Consider the omega-limit w of this set of strings. The states attained when generating w eventually correspond to the plant states XB and FB and to the specification state B. In the product generator, the states must be part of an SCC. Furthermore, since B is not marked there must exists an SCC with no specification-marked state. However, this SCC also contains a state that coresponds to XB, which is marked by the plant. Thus, the procedures return "false".

Parameter Conditions:

This implementation requires the alphabets of both generators to match. Furthermore, both specified generators must be deterministic and trim (w.r.t. Buechi acceptance).

BuechiProduct

Product composition for Buechi acceptance condition.

Detailed description:

Given two Buechi automata G1 and G2, this function computes an automaton GRes such that

L(GRes) = L(G1) ∩ L(G2)
Bm(GRes) = Bm(G1) ∩ Bm(G2)

The implementation is similar to that of Parallel, except that we augment the state set to hold an extra flag to track when G1 attains a marking after G2 did so. This enables the construction of a a set of marked states for GRes that when passed infinitely often implies that this also was the case for G1 and G2.

Parameter Conditions:

The alphabets of both arguents must match. Arguments are required to be deterministic, and so will be the result. In this implementation, only accessible states are generated. It is considered an error if the controllability flags in the arguments don't match.

BuechiParallel

Parallel composition with relaxed acceptance condition.

Detailed description:

The marking introduced by the ordinary Parallel composition requires that each component attains a marked state simultaneously. This condition may turn out too restrictive when focus is on the infinite time behaviour.

The function BuechiParallel relaxes the acceptance condition, in that it requires each component always to eventually accept the generated prefix, but not necessarily simultaneously with the other component:

L(GRes) = L(G1) || L(G2)
Bm(GRes) = Bm(G1) || Bm(G2)
     := {w ∈ Sigma^w| P1(w) ∈ Bm(G1) and P2(w) ∈ Bm(G2) }

where P1 and P2 denote the natural projections on the respective alphabet.

Technically, BuechiParallel constructs its result on the product of the state spaces of G1 and G2 with an additional boolean flag. The flag is used to mark those states in GRes that correspond to a G2-marking with most recent marking in G1. Thus, a trajectory that passes a GRes-marking infinitely often, also passes infinitely many marked states in G1 and G2.

Example:

Component G1 Component G2

Composition G=G1 ||| G2

Parameter Conditions:

In this implementation, only accessible states are generated. Arguments are required to be deterministic, and so will be the result. It is considered an error if the controllability flags in the arguments don't match.