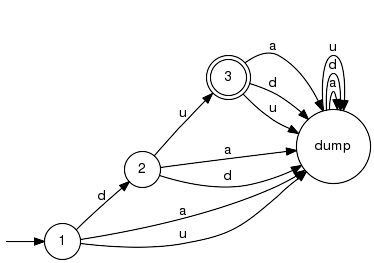
Misc Functions on Generators

EmptyLanguage

Set generator to mark empty language.

Detailed description:

Returns a generator G with the specified alphabet Sigma, no states and no transitions; i.e., we have Lm(G) = L(G) = 0.

Parameter Conditions:

The empty language generator is deterministic.

IsEmptyLanguage

Test Generator G for empty marked language Lm(G).

Parameter Conditions:

The argument may be non-deterministic.

Automaton

Convert generator to formal automaton.

Detailed description:

Converts the given generator G to a formal automaton that marks the same marked language Lm(G) while accepting any input string, i.e. L(G) = Sigma*. This is achieved by introducing a dump state to represent Sigma*-Closure(Lm(G)).

Note. In libFAUDES pre 2.33, we used to preprocess by Trim in order to gain performance. This was dropped so you may want to invoke Trim explicitly. The rational was to become agnostic to alternative acceptance conditions.

Example:

G	GRes

Parameter Conditions:

The provided generator is assumed to be deterministic. The resulting generator is guaranteed to be deterministic.

IsClosed

Tests a language for being prefix-closed.

Detailed description:

A language L is prefix-closed if for each string s ∈ L all prefixes r ≤ s are also element of L:

s ∈ L and r ≤ s    ⇒    r ∈ L.

The function IsClosed tests whether the language Lm(G) marked by the specified generator G is prefix-closed. It does so by testing whether any state that is accessible and co-accessible also is marked. For deterministic generators, this condition is sufficient and necessary. In general, it is only sufficient.

Example:

G

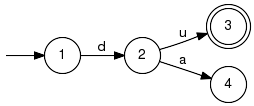
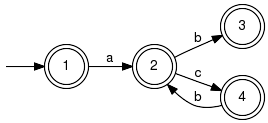
The language Lm(G) marked by the above generator is not prefix-closed, since the states 1, 2 and 4 are accessible and co-accessible but not marked. For example, the string ac ∉ Lm(G) is a prefix of acbb ∈ Lm(G).

PrefixClosure

Compute prefix closure for given language.

Detailed description:

For any language L there exists a smallest prefix-closed superset, the so-called prefix-closure of L:

Closure(L) := {r ∈ Sigma*| ∃ s ∈ L : r ≤ s}.

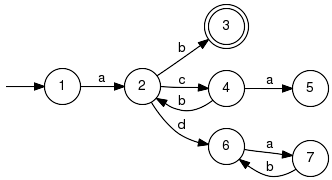
This function computes a realisation of the prefix-closure of Lm(GArg) by first erasing all states that are not co-accessible and then marking the remaining states.

Example:

G	GRes

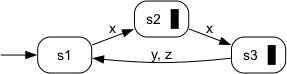
ApplyRelabelMap

Relabel events/transitions as specified by a set-values map.

Detailed description:

An RelabelMap is a set valued map with domain and range EventSet. It is used to represent re-labeling a scheme. To maintain an event, it must be excluded from the domain. To remove an event, it shall be mapped to the empty set. For a one-to-one replacement, use singleton target sets. Examples are given in the Lua-faudes tutorials 1_containers.lua and 2_generators.lua.

Example:

The figure shows the scheme "a->x, b->{z,y} and c->{}".

G	GRes