Controllable Sublanguages

Functions related to the notion of controllability and (basic) supervisory control.

Definition of Controllability

The notion of controllability was originally introduced by P.J. Ramadge and W.M. Wonham, e.g. [S1]:

Consider two languages L and K over a common alphabet Sigma, and a set of uncontrollable events Sigma_uc ⊆ Sigma. Then K is said to be controllable w.r.t. (L,Sigma_uc) iff

Closure(K)Sigma_uc ∩ Closure(L)  ⊆  Closure(K)

The definition addresses the situation where K is the closed-loop behaviour that has been achieved by supervision of a plant L. Whenever, after some past string s ∈ Closure(K), the uncontrollable event o ∈ Sigma_uc is accepted by the plant Closure(L), it must also be accepted by the controller and, hence, cannot be rejected in the closed loop Closure(K).

Controller Synthesis

For the purpose of controller synthesis, consider a plant L ⊆ Sigma*, a specification E ⊆ Sigma*, and, uncontrollable events Sigma_uc ⊆ Sigma. The task then is to find a prefix closed controller H ⊆ Sigma*, such that

(1)     L and H are non-blocking, i.e., Closure(L ∩ H) = Closure(L) ∩ H ;
(2)     the controller H is controllable w.r.t. (L,Sigma_uc) ; and,
(3)     the closed-loop behaviour satisfies the specification, i.e., L ∩ H ⊆ E.

For any prefix closed controller H which satisfies the above conditions, the closed loop K = L ∩ H exhibits the following properties:

(a)     K is relatively closed w.r.t. L, i.e., K = L ∩ Closure(K);
(b)     K is controllable w.r.t. (L,Sigma_uc);
(c)     K ⊆ E.

Moreover, if a language K satisfies (a)-(c), the controller H = Closure(K) solves the synthesis problem.

A fundamental result presented in [S1] is that all of the conditions (a)-(c) are retained under arbitrary union. Thus, the set of all achievable closed-loop behaviours forms a complete upper semi-lattice. In particular, the supremum

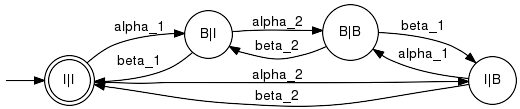
K↑ = sup{ K ⊆ E | K is controllable w.r.t. (L,Sigma_uc) and K is relatively closed w.r.t. L}

exists uniquely and itselfs satisfies conditions (a)-(c). It is referred to as the closed-loop behaviour under minimal restrictive supervision and it is commonly used to implement the least restrictive controller H↑ = Closure(K↑).

An example is given at the main page of the Synthesis plug-in.

Note 1: In the literature the supervisor is commonly represented by a map V that maps past observations s ∈ Closure(L) to control patterns V(s) = \gamma, Sigma_uc ⊆ \gamma ⊆ Sigma. The closed-loop behaviour of L under supervison V is then defined by the condition, that at each instance of time an event can only occur if it complies with the plant behaviour and the current control pattern. However, for the scope of this documentation, we feel that a simplified presentation purely in terms of languages is preferable.

Note 2: For the above problem of controller synthesis the plant is represented as a single language L. For the situation, where the plant is more adequatly modelled by a generator that fails to be nonblocking, i.e. L(G) ≠ Closure(Lm(G)), one may proceed with L = L(G) and employ a specification E ⊆ Lm(G) to design a marking controller that avoids blocking; see also SupConNB.

IsControllable

Tests controllablity condition.

Signature:

IsControllable(+In+ Generator GPlant, +In+ EventSet ACntrl, +In+ Generator GCand, +Out+ Boolean BRes)

IsControllable(+In+ System GPlant, +In+ Generator GCand, +Out+ Boolean BRes)

Detailed description:

This function tests controllability of L(GCand) w.r.t. (L(GPlant),Sigma_uc). The set of uncontrollable events Sigma_uc is either taken from the plant event attributes or specified as the complement of the parameter ACntrl.

Since the definition of controllability exclusively refers to the closure of the relevant languages, this function can be also used to test controllability of Lm(GCand) w.r.t. (Lm(GPlant),Sigma_uc), provided that the specified generators are nonblocking. This can be achieved by applying Trim before calling IsControllable.

The current implementation performs the test by inspecting the transitions in the product composition GPlant x GCand. If GCand disables a transition in GPlant that is labled with an uncontrollable event, the function returns "false". Else, it returns "true".

Example:

Consider the very simple machine scenario. We have

Overall Plant GPlant
Product(GPlant,GSpec)

In the product composition, the state B|B|F disables the uncontrollable event beta_1 since the buffer is full and cannot take any workpiece. However, in the corresponding plant state B|B, the event beta_1 is enabled, since machine M1 is busy and may on completion pass on the workpiece. Thus, the specification is not controllable w.r.t. the plant and the function IsControllable returns "false" when applied to GPlant and GSpec.

Parameter Conditions:

This implementation requires the alphabets of plant and specification to match. Furthermore, both generators must be deterministic. Effectively, the specification is intersected with the plant language.

SupConClosed

Computes the supremal controllable sublanguage.

Signature:

SupConClosed(+In+ System GPlant, +In+ Generator GSpec, +Out+ Generator GSupervisor)

SupConClosed(+In+ Generator GPlant, +In+ EventSet AContr, +In+ Generator GSpec, +Out+ Generator GSupervisor)

Detailed description:

Given a plant L = L(GPlant) and a specification E = L(GSpec), this function computes the supremal controllable and closed sublanguage K ⊆ E∩L:

K↑ = sup{ K ⊆ E∩L | K is controllable w.r.t. (L,Sigma_uc)  and prefix closed } .

Note that, since E is prefix closed, the above supremum is equivalently characterised by

K↑ = sup{ K ⊆ E∩L | K is controllable w.r.t. (L,Sigma_uc) } .

The result is returned as an accessible and deterministic (but in general blocking) generator GSupervisor that generates K↑. The set of uncontrollable events Sigma_uc is either taken from the plant generator's event attributes or specified as the complement of the parameter ACntrl. See e.g. [C2] for the base algorithm used in the implementation of this function.

Clearly, K↑ satisfies the closed-loop conditions (a)-(c). In particular, H = K↑ solves the synthesis problem.

Example:

For very-simple machine example, it happens that SupConClosed returns the same generator as SupConNB does. However, for SupConClosed the result is interpreted as the generated language.

Parameter Conditions:

This implementation requires the alphabets of plant and specification to match. Furthermore, both generators must be deterministic. Effectively, the specification is intersected with the plant language.

SupConNB

Computes the supremal controllable sublanguage.

Signature:

SupConNB(+In+ System GPlant, +In+ Generator GSpec, +Out+ Generator GSupervisor)

SupConNB(+In+ Generator GPlant, +In+ EventSet AContr, +In+ Generator GSpec, +Out+ Generator GSupervisor)

Detailed description:

Given a plant realisation G (argument GPlant) and a specification E = Lm(GSpec), this function computes the supremal controllable sublanguage K↑ ⊆ E∩Lm(G):

K↑ = sup{ K ⊆ E∩Lm(G) | K is controllable w.r.t. (L(GPlant),Sigma_uc) } .

Note that, if G is non-blocking, the above supremum is equivalently characterised by

K↑ = sup{ K ⊆ E∩Lm(G) | K is controllable w.r.t. (Lm(G),Sigma_uc) } .

The result is returned as a trim deterministic generator GSupervisor that marks K↑. The set of uncontrollable events Sigma_uc is either taken from the plant generator's event attributes or specified as the complement of the parameter ACntrl. See e.g. [C2] for the base algorithm used in the implementation of this function.

For the synthesis problem in this documentation, we assume that G is non-blocking. Here, K↑ satisfies the closed-loop conditions (b) and (c). In addition, K↑ can be observed to be relatively prefix-closed w.r.t. E. If the specification E is relatively marked w.r.t. the plant Lm(G) (see also IsRelativelyMarked), this implies that K↑ is relatively prefix-closed w.r.t. Lm(G), i.e., K↑ also fulfills the closed-loop condition (a) and the controller H = Closure(K↑) solves the synthesis problem.

If the specification E fails to be relatively marked w.r.t. the plant L, one may replace E with the supremal sublanguage that is relatively closed (see also SupRelativelyPrefixClosed) before invoking SupConNB, to obtain

E⇧ = sup{ K ⊆ E | K is relatively closed w.r.t. Lm(G) }
K⇧ = sup{ K ⊆ E⇧ ∩Lm(G) | K is controllable w.r.t. (Lm(G),Sigma_uc) } .

By the above considerations, this will result in the supremal language K⇧, that satisfies all three closed-loop conditions (a)-(c).

Alternatively, one may resort to a so called marking supervisor H = K↑ that only satisfies conditions (b) and (c). From H ⊆ L, the marking of the supervisor implies the marking of the plant and we can implement the closed loop as the intersection Closure(L)∩H, hence the notion of a marking supervisor. The nonblocking condition then becomes formally Closure(Closure(L)∩H) = Closure(L)∩Closure(H), which, by H ⊆ L, is trivially satisfied.

Example:

The supervisor given for the very-simple machine example has been obtained by SupConNB. It failes to be relatively-closed and thus is interpreted as a marking supervisor.

Parameter Conditions:

This implementation requires the alphabets of plant and specification to match. Furthermore, both generators must be deterministic. Effectively, the specification is intersected with the plant language.

IsRelativelyPrefixClosed

Test for relative prefix-closedness.

Signature:

IsRelativelyPrefixClosed(+In+ Generator GPlant, +In+ Generator GCand, +Out+ Boolean BRes)

Detailed description:

A language K is relatively closed w.r.t. a language L, if K can be recovered from its closure and L. Formally:

K = Closure(K) ∩ L .

This function tests, whether

Lm(GCand) = L(GCand) ∩ Lm(GPlant)

by performing the product composition of the two generators in order to verify the following two conditions:

  • L(GCand) ⊆ L(GPlant), and

  • (∀  accessible states (qPlant,qCand)) [ qCand ∈ QCand_m  ⇔  qPlant ∈ QPlant_m ] .

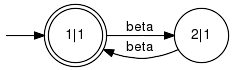
Here, QPlant_m and QCand_m refer to the marked states of GPlant and GCand, respectively. The function returns "true" if both conditions are fulfilled.

Example:

Consider the very simple machine scenario.

Overall Plant GPlant
Supervisor GSupervisor

The string alpha_1 beta_1 is within the languages generated by the supervisor and the plant respectively. It is not within the language marked by the supervisor, since that language is a subset of the language marked by the specification and thus requires the buffer to be empty. In particular, the string alpha_1 beta_1 witnesses a violation of relative closedness condition and the function IsRelativelyPrefixClosed returns "false" when applied to GPlant and GSupervisor.

Parameter Conditions:

This implementation requires the alphabets of both generators to match. Furthermore, both specified generators must be deterministic and nonblocking.

IsRelativelyMarked

Test for relative marking.

Signature:

IsRelativelyMarked(+In+ Generator GPlant, +In+ Generator GCand, +Out+ Boolean BRes)

Detailed description:

A language K is relatively marked w.r.t. a language L, if its marking is implied by L. Formally:

K ⊇ Closure(K) ∩ L .

This function tests, whether

Lm(GCand) ⊇ L(GCand) ∩ Lm(GPlant)

by performing the product composition of the two generators in order to verify the following condition:

  • (∀  accessible states (qPlant,qCand)) [ qCand ∈ QCand_m  ⇐  qPlant ∈ QPlant_m ] .

Here, QPlant_m and QCand_m refer to the marked states of GPlant and GCand, respectively. The function returns "true" if the condition is fulfilled.

Example:

Consider the very simple machine scenario; see also IsControllable.

In the product composition of plant and specification the state I|I|F is not marked, since the specification required the buffer to be empty. However, the corresponding I|I plant state is marked. The string alpha_1 beta_1 therefore is in Lm(GPlant)∩L(GSpec) but not in Lm(GSpec). Thus, the condition is violated and the function IsRelativelyMarked returns "false" when applied to GPlant and GSpec.

Parameter Conditions:

This implementation requires the alphabets of both generators to match. Furthermore, both specified generators must be deterministic and nonblocking.

SupRelativelyPrefixClosed

Computes the supremal relatively prefix-closed sublanguage.

Signature:

SupRelativelyPrefixClosed(+In+ Generator GPlant, +In+ Generator GSpec, +Out+ Generator GRes)

Detailed description:

Given a plant L = Lm(GPlant) and a specification E = Lm(GSpec), this function computes the supremal sublanguage K↑ ⊆ E that is relatively prefix-closed w.r.t. L:

K↑ = sup{ K ⊆ E| K = Closure(K) ∩ L } .

Note that K↑ ⊆ L∩E. The current implementation starts with the product GPlant x GSpec as a first candidate. It then subsequently removes states that correspond to a marked state in GPlant and to an unmarked state in GSpec. The result is returned as a trim deterministic generator GRes that marks K↑.

For a formal discussion on relative-closedness in the context of supervisory control, including a formula for the supremal relatively closed sublanguage, see [S9].

Example:
Plant L Specification E Result K↑
Parameter Conditions:

This implementation requires the alphabets of both generators to match. Furthermore, both specified generators must be deterministic.

libFAUDES 2.32b --- 2024.03.01 --- with "synthesis-observer-observability-diagnosis-hiosys-iosystem-multitasking-coordinationcontrol-timed-simulator-iodevice-luabindings-hybrid-example-pybindings"

>>