|
|
The multitasking plug-in allows to examine colored marking generators (CMGs). Generators can be created in the same way as in the standard implementation, the identifier is MtcSystem. In addition to the standard implementation that is based on the classical theory, colored markings can be applied to single states. The class faudes::TmtcGenerator implements various methods to handle CMGs. Furthermore, functions for making CMGs deterministic or strongly coaccessible, for computing the parallel composition or an projection, are provided.
The libFAUDES multitasking plugin allows to develop descrete event systems using the classical, monolithic approach. Additionally, it is suitable for their modular or hierarchical development. For more information to the modular proceeding see
"Modular Multi-tasking Supervisory Control of Composite Discrete Event Systems", M.H. de Queiroz and J.E.R. Cury, IFAC World Congress, 2005.
Further information to the hierarchical proceeding can be found in
"Hierarchical and Decentralized Multitasking Control of Discrete Event Systems", K. Schmidt, M. H. Queiroz, and J. E. R. Cury, IEEE Conference on Decision and Control, 2007.
License
The implementation of the multitasking plug-in was part of Matthias Singers' student project, supervised by Klaus Schmidt. The code is distributed with libFAUDES and under the terms of the LGPL.
Copyright (c) 2008, Matthias Singer.
|
| Idx | faudes::calcNaturalObserver (const MtcSystem &rGen, EventSet &rHighAlph) |
| |
| bool | faudes::IsMtcObs (const MtcSystem &rLowGen, const EventSet &rHighAlph) |
| |
| void | faudes::mtcParallel (const MtcSystem &rGen1, const MtcSystem &rGen2, MtcSystem &rResGen) |
| |
| void | faudes::mtcDeterministic (const MtcSystem &rGen, MtcSystem &rResGen) |
| |
| void | faudes::mtcProjectNonDet (MtcSystem &rGen, const EventSet &rProjectAlphabet) |
| |
| void | faudes::mtcProjectNonDet (const MtcSystem &rGen, const EventSet &rProjectAlphabet, MtcSystem &rResGen) |
| |
| void | faudes::mtcProject (const MtcSystem &rGen, const EventSet &rProjectAlphabet, MtcSystem &rResGen) |
| |
| void | faudes::mtcInvProject (MtcSystem &rGen, const EventSet &rProjectAlphabet) |
| |
| bool | faudes::ComputeSCC (const Generator &rGen, std::set< StateSet > &rSCCSet, StateSet &rRoots) |
| |
| void | faudes::ColoredSCC (MtcSystem &rGen, ColorSet &rColors, std::set< StateSet > &rColoredSCCs) |
| |
| bool | faudes::CheckRedundantColor (MtcSystem rGen, Idx redundantColor) |
| |
| void | faudes::OptimalColorSet (const MtcSystem &rGen, ColorSet &rOptimalColors, EventSet &rHighAlph) |
| |
| void | faudes::mtcSupCon (const MtcSystem &rPlantGen, const MtcSystem &rSpecGen, MtcSystem &rResGen) |
| |
| void | faudes::mtcSupConClosed (const MtcSystem &rPlantGen, const MtcSystem &rSpecGen, MtcSystem &rResGen) |
| |
◆ calcNaturalObserver()
Calculate a colored natural observer by extending a given high-level alphabet. This function extends a given high-level alphabet such that the corresponding natural projection becomes a colored observer for a given colored marking generator. The function calls the function ExtendHighAlphabet in the Observer plugin.
- Parameters
-
| rGen | input colored marking generator |
| rHighAlph | high-level alphabet that is extended towards a colored observer |
- Returns
- number of states of the high-level colored marking generator
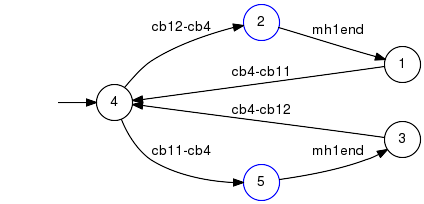
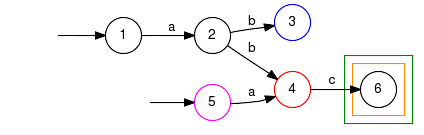
Example: Computation of an Lm-observer
| Original generator |
|
|
| Original high-level alphabet (rHighAlph): cb4-cb12, cb12-cb4, cb11-cb4, cb4-cb11 |
|
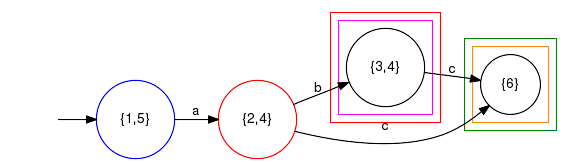
| Result of calcNaturalObserver(rGenObs, rHighAlph); |
| New high-level alphabet (rNewHighAlph): cb4-cb12, cb12-cb4, cb11-cb4, cb4-cb11, mh1end |
|
|
|
Definition at line 41 of file mtc_observercomputation.cpp.
◆ CheckRedundantColor()
Check if a color in a colored marking generator is redundant for the supervisor synthesis. This function determines if a color can be removed from a CMG if it is redundant for the supervisor synthesis. The algorithm implements the work in K. Schmidt and J.E.R. Cury, "Redundant Colors in the Multitasking Supervisory Control for Discrete
Event Systems", Workshop on Dependable Control of Discrete Event Systems, 2009.
- Parameters
-
| rGen | Reference to generator |
| redundantColor | Index of the color to be removed
|
- Returns
- true if the color can be removed, false otherwise
Definition at line 172 of file mtc_redundantcolors.cpp.
◆ ColoredSCC()
Compute all strongly connected components (SCCs) in a colored marking generator (CMG) that are marked with a given set of colors. This function finds all SCCs in a CMG that contain states with all colors in a given color set. To find all SCCs, first the function ComputeSCC is called.
- Parameters
-
| rGen | generator under investigation |
| rColors | colors that have to be contained in the SCCs |
| rColoredSCCs | SCCs marked with all colors in rColors |
Definition at line 140 of file mtc_redundantcolors.cpp.
◆ ComputeSCC()
Computes the strongly connected components (SCCs) of an automaton. This function is the wrapper function for Trajan's algorithm that is implemented in the function SearchSCC.
- Parameters
-
| rGen | investigated generator |
| rSccSet | Set of strongly connected components (result). |
| rRoots | Set of states that each are root of some SCC (result). |
- Returns
- true if SCCs have been found, false if not.
Definition at line 121 of file mtc_redundantcolors.cpp.
◆ IsMtcObs()
Verification of the observer property. For verifying if a natural projection has the observer property, one step in the observer algorithm is evaluated. If the resulting generator equals the input generator, then the natural projection on the abstraction alphabet is an observer.
- Parameters
-
| rLowGen | Input generator |
| rHighAlph | High level alphabet |
- Returns
- true if the observer property holds
Definition at line 39 of file mtc_obserververification.cpp.
◆ mtcDeterministic()
Make generator deterministic. (function wrapper)
- Parameters
-
| rGen | Reference to generator |
| rResGen | Reference to resulting deterministic generator |
Example: Converting a nondeterministic MtcSystem to a deterministic one
| Original MtcSystem gen |
|
|
| The MtcSystem contains two initial states and, leaving from state 2, it has two transitions containing the same event b which are leading to two separate states. |
|
| Result of the deterministic operation |
|
|
| Both initial states are combined to a single one. All color labels appearing in all original states are adapted to the new initial state. Furthermore, states are merged in that way that the generator's language stays the same, but the generator gets deterministic. |
|
Definition at line 73 of file mtc_project.cpp.
◆ mtcInvProject()
Inverse projection. This adds selfloop transition at every state for all missing events.
- Parameters
-
| rGen | Reference to generator |
| rProjectAlphabet | Alphabet for inverse projection |
Example: Inverse projection of an MtcSystem for a specified alphabet which is larger than the MtcSystem's one.
| Original MtcSystem |
|
|
| The projection alphabet contains the events {a, b, c}. |
|
| Result of the projection |
|
|
| Events, that are not part of the MtcSystem's alphabet are inserted as self-loops into every state. |
|
Definition at line 498 of file mtc_project.cpp.
◆ mtcParallel()
Parallel composition of two colored marking generators, controllability status is observed
- Parameters
-
| rGen1 | First MtcSystem for parallel composition |
| rGen2 | Second MtcSystem for parallel composition |
| rResGen | MtcSystem in which the result of the parallel composition is saved |
Example: Parallel composition of two colored marking generators
| MtcSystems for composition |
|
|
|
|
| The left MtcSystem contains only one colored state, state 2, whereas the right one possesses two color labels - one for each state. |
|
| Result of the parallel composition |
|
|
| The composed MtcSystem contains all colors that appear in both single MtcSystems.The single states are labeled with a color when both states to combine are labeled with it. A color label is also added when it occurs in one of the two currently regarded states to compose and, at the same time, it does not appear in the second single MtcSystem. |
|
Definition at line 32 of file mtc_parallel.cpp.
◆ mtcProject()
Minimized Deterministic projection. This function does not modify the MtcSystem. It calls project, determine and statemin.
- Parameters
-
| rGen | Reference to generator |
| rProjectAlphabet | Projection alphabet |
| rResGen | Reference to resulting deterministic generator |
Example: Projection of an MtcSystem to a specified alphabet
| Original MtcSystem gen |
|
|
| The projection alphabet contains the events {a, b, d}. |
|
| Result of the projection |
|
|
| The resulting MtcSystem contains all events that appear in the oringinal MtcSystem and in the specified alphabet. Moreover, the resulting MtcSystem is deterministic. |
|
Definition at line 421 of file mtc_project.cpp.
◆ mtcProjectNonDet() [1/2]
Project generator to alphabet rProjectAlphabet
- Parameters
-
| rGen | Reference to generator |
| rProjectAlphabet | Projection alphabet |
| rResGen | Reference to result |
Definition at line 415 of file mtc_project.cpp.
◆ mtcProjectNonDet() [2/2]
Project generator to alphabet rProjectAlphabet
- Parameters
-
| rGen | Reference to generator |
| rProjectAlphabet | Projection alphabet |
Definition at line 328 of file mtc_project.cpp.
◆ mtcSupCon()
Nonblocking Supremal Controllable Sublanguage (wrapper function)
Computes symbolic state names in resulting supervisor automaton if symbolic state names are enabled in rPlantGen and rSpecGen
- Parameters
-
| rPlantGen | Plant MtcSystem |
| rSpecGen | Specification MtcSystem |
| rResGen | Reference to resulting MtcSystem, the minimal restrictive nonblocking supervisor |
- Exceptions
-
| Exception |
- Alphabets of generators don't match (id 500)
- plant nondeterministic (id 501)
- spec nondeterministic (id 503)
- plant and spec nondeterministic (id 504)
|
Example: Synthesis of a strongly nonblocking supervisor for a model and a corresponding specification
| Model MtcSystem |
|
|
| The model contains one state that results in a blocking behavior. |
| Specification MtcSystem |
|
|
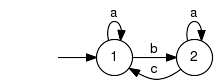
| The specification expresses, that after an event b an event c has to occur before b can happen again. Furthermore, it forbids that event c occurs before event b has taken place.Before being able to compute a supervisor, an inverse projection step has to be applied on the specification. It inserts self-loops for event a in both states, as the alphabets of model and specification must be identical. |
|
| Strongly nonblocking supervisor |
|
|
| The synthesized supervisor ensures that the specification condition is fulfilled. That is why state 5 of the model and the corresponding transitions are erased. Observe that the operation does not make a generator nonblocking, as is shown in the example where state 3 is still existing. |
|
Definition at line 41 of file mtc_supcon.cpp.
◆ mtcSupConClosed()
Supremal Controllable Sublanguage (wrapper function)
- Parameters
-
| rPlantGen | Plant MtcSystem |
| rSpecGen | Specification MtcSystem |
| rResGen | Reference to resulting MtcSystem, the minimal restrictive supervisor |
- Exceptions
-
| Exception |
- Alphabets of generators don't match (id 500)
- plant nondeterministic (id 501)
- spec nondeterministic (id 503)
- plant and spec nondeterministic (id 504)
|
Example: Synthesis of a multitasking supervisor for a model and a corresponding specification. Supervisor does not take care of nonblocking behavior.
| Model MtcSystem |
|
|
| The model contains one state that results in a blocking behavior. |
| Specification MtcSystem |
|
|
| The specification expresses, that after an event b an event c has to occur before b can happen again. Furthermore, it forbids that event c occurs before event b has taken place.Before being able to compute a supervisor, an inverse projection step has to be applied on the specification. It inserts self-loops for event a in both states, as the alphabets of model and specification must be identical. |
|
| Strongly nonblocking supervisor |
|
|
| The supervisor synthesized by this function is strongly nonblocking. Of course, it ensures that the specification condition is fulfilled. |
|
Definition at line 130 of file mtc_supcon.cpp.
◆ OptimalColorSet()
Compute an optimal subset of the colors that should be removed. This function tries to find an optimal subset of colors that can be removed from the given colored marking generator without affecting supervisor synthesis. Here, optimality is defined w.r.t. the smallest number of states of a high-level generator after removing the colors.
- Parameters
-
| rGen | input colored marking generator |
| rOptimalColors | optimal color set to be removed |
| rHighAlph | hgh-level alphabet for hierarchical abstraction after color removal. Initially, the alphabet should contain all events that must be present in the high-level alphabet |
<>
Definition at line 242 of file mtc_redundantcolors.cpp.
libFAUDES 2.33l
--- 2025.09.16
--- c++ api documentaion by doxygen
|