| |
|
||||||
|
|
|||||||
Detailed DescriptionThis module collects general purpose functions on Generator, System, EventSet and Alphabet typed data. It includes functions related to regular expressions, projection, parallel composition, etc.
Function Documentation◆ Accessible() [1/2]
RTI wrapper function. See also vGenerator::Accessible(). Definition at line 3925 of file cfl_generator.cpp. ◆ Accessible() [2/2]
RTI wrapper function. See also vGenerator::Accessible(). Definition at line 3920 of file cfl_generator.cpp. ◆ aDeterministic()
Make generator deterministic. See also Deterministic(const Generator&, Generator&). This version maintains event attributes provided they can be castes to the result type.
Definition at line 77 of file cfl_determin.cpp. ◆ aInvProject() [1/2]
Inverse projection. This adds selfloop transition at every state for all missing events. This version tries to be transparent to attributes.
Definition at line 1524 of file cfl_project.cpp. ◆ aInvProject() [2/2]
Inverse projection. This adds selfloop transition at every state for all missing events. This version tries to be transparent to attributes.
Definition at line 1504 of file cfl_project.cpp. ◆ AlphabetExtract()
RTI wrapper function. Definition at line 3992 of file cfl_generator.cpp. ◆ AlphabetLanguage()
Alphabet Language, L(G)=Lm(G)=Sigma. Construct generator generating and marking an alphabet as languages, that is L(G)=Lm(G)=Sigma. Method: this function creates a generator with one init state and one marked state. For each event from rAlphabet, a transition is inserted leading from the init state to the marked state. No restrictions on parameters.
Example:
Definition at line 718 of file cfl_regular.cpp. ◆ aOmegaParallel()
Parallel composition with relaxed acceptance condition. See also OmegaParallel(const Generator&, const Generator&, Generator&). This version tries to be transparent on event attributes: if argument attributes match and if the result can take the respective attributes, then they are copied; it is considered an error if argument attributes do not match.
Definition at line 226 of file cfl_omega.cpp. ◆ aOmegaProduct()
Product composition for Buechi automata. See also OmegaProduct(const Generator&, const Generator&, Generator&). This version tries to be transparent on event attributes: if argument attributes match and if the result can take the respective attributes, then they are copied; it is considered an error if argument attributes do not match.
Definition at line 67 of file cfl_omega.cpp. ◆ aParallel() [1/2]
Parallel composition. See also Parallel(const Generator&, const Generator&, Generator&). This version tries to be transparent on event attributes: if argument attributes match and if the result can take the respective attributes, then they are copied; it is considered an error if argument attributes do not match.
Definition at line 51 of file cfl_parallel.cpp. ◆ aParallel() [2/2]
Parallel composition. See also Parallel(const Generator&, const Generator&, Generator&). This version fills a composition map to map pairs of old states to new states.
Definition at line 125 of file cfl_parallel.cpp. ◆ aProduct() [1/2]
Product composition. See also Product(const Generator&, const Generator&, Generator&). This version tries to be transparent on event attributes: if argument attributes match and if the result can take the respective attributes, then they are copied; it is considered an error if argument attributes do not match.
Definition at line 426 of file cfl_parallel.cpp. ◆ aProduct() [2/2]
Product composition. See also Product(const Generator&, const Generator&, Generator&). This version fills a omposition map to map pairs of old states to new states.
Definition at line 460 of file cfl_parallel.cpp. ◆ aProject()
Deterministic projection. See also Project(const Generator&, const EventSet&, Generator&). This version tries to be transparent on event attributes: if argument attributes match and if the result can take the respective attributes, then they are copied; it is considered an error if argument attributes do not match.
Definition at line 1417 of file cfl_project.cpp. ◆ aProjectNonDet()
Language projection. See also ProjectNonDet(const Generator&, const EventSet&). This version tries to be transparent on event attributes: result maintains its attributes.
Definition at line 1411 of file cfl_project.cpp. ◆ aStateMin() [1/2]
State set minimization. See also StateMin(const Generator&, Generator&). This version maintains event attributes provided they can be casted to the result type.
Definition at line 629 of file cfl_statemin.cpp. ◆ aStateMin() [2/2]
State set minimization. See also StateMin(const Generator&, Generator&). This version maintains event attributes provided they can be casted to the result type.
Definition at line 635 of file cfl_statemin.cpp. ◆ Automaton() [1/2]
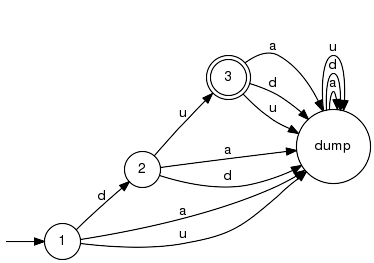
Convert generator to automaton. Convert a generator marking the language Lm into a formal automaton recognizing Lm with a dump state representing Sigma*-PrefixClosure(Lm). In this function, Sigma is given by the alphabet of rGen; see also Automaton(rGen,rAlphabet). For information about automata, see [Wonham. Supervisory Control of Discrete Event Systems]. The original generated language is ignored. Note: An automaton is a deterministic transition structure according to the formal definition; see also "Determinism" below. Method: Uncoaccessible states are erased, as the language generated by rGen is not examined in this function. A dump state representing "Sigma*-PrefixClosure(Lm)" is created. Then, the transition relation is completed such that it is fully defined for each state and each event. Formerly undefined transitions lead to the dump state. Determinism: Input parameter has to be deterministic for correct result. If not, then the (also nondeterministic) result recognizes the correct language, but the dump state does not represent "Sigma*-PrefixClosure(Lm)" as it should; see also example ExAutomaton_basic(). If FAUDES_CHECKED is defined a warning on non-deterministic input is issued. No further restrictions on parameter.
Example:
Definition at line 454 of file cfl_regular.cpp. ◆ Automaton() [2/2]
Convert generator to automaton wrt specified alphabet. Convert a generator marking the language Lm into a formal automaton recognizing Lm with a dump state representing Sigma*-PrefixClosure(Lm(rGen)). In this function, Sigma is given by the parameter rAlphabet. For information about automata, see [Wonham. Supervisory Control of Discrete Event Systems]. The original generated language is ignored. Note: An automaton is a deterministic transition structure according to the formal definition; see also "Determinism" below. Method: Uncoaccessible states are erased, as the language generated by rGen is not examined in this function. A dump state representing "Sigma*-PrefixClosure(Lm)" is created. Then, the transition relation is completed such that it is fully defined for each state of rGen and each event of rAlphabet. Formerly undefined transitions lead to the dump state. Determinism: Input parameter has to be deterministic for correct result. If not, then the (also nondeterministic) result recognizes the correct language, but the dump state does not represent "Sigma*-PrefixClosure(Lm)" as it should; see also example ExAutomaton_basic(). If FAUDES_CHECKED is defined a warning on non-deterministic input is issued. No further restrictions on parameters.
Definition at line 339 of file cfl_regular.cpp. ◆ Coaccessible() [1/2]
RTI wrapper function. See also vGenerator::Coaccessible(). Definition at line 3936 of file cfl_generator.cpp. ◆ Coaccessible() [2/2]
RTI wrapper function. See also vGenerator::Coaccessible(). Definition at line 3931 of file cfl_generator.cpp. ◆ Complete() [1/4]
RTI wrapper function. See also vGenerator::Complete(). Definition at line 3958 of file cfl_generator.cpp. ◆ Complete() [2/4]
RTI wrapper function. See also vGenerator::Complete(). Definition at line 3947 of file cfl_generator.cpp. ◆ Complete() [3/4]
RTI wrapper function. See also vGenerator::Complete(). Definition at line 3942 of file cfl_generator.cpp. ◆ Complete() [4/4]
RTI wrapper function. See also vGenerator::Complete(). Definition at line 3953 of file cfl_generator.cpp. ◆ ComputeBisimulation() [1/3]
Computation of the coarsest bisimulation relation for a specified generator. This is a convenience wrapper for ComputeBisimulation(Generator&, std::map<Idx,Idx>&) to return a list of nontrivial equivalence classes (singletons are not reported) See ComputeBisimulation(const Generator&, std::map<Idx,Idx>).
Definition at line 1306 of file cfl_bisimulation.cpp. ◆ ComputeBisimulation() [2/3]
Computation of the coarsest bisimulation relation for a specified generator. This funtcion creates an instance of the class Bisimulation and triggers the computation of the coarsest quasi-congruence on the given generator by calling the function Bisimulation::partition. The result is returned as a map from original state idicess to partion indicees. The implementation is derived from J.-C. Fernandez, “An implementation of an efficient algorithm for bisimulation equivalence,” Science of Computer Programming, vol. 13, pp. 219-236, 1990. This interface is neither used nor tested. Use ComputeBisimulation(Generator& , std::map<Idx,Idx>& , Generator& ) instead.
Definition at line 1272 of file cfl_bisimulation.cpp. ◆ ComputeBisimulation() [3/3]
Computation of the coarsest bisimulation relation for a specified generator. This is a convenience wrapper for ComputeBisimulation(Generator&, std::map<Idx,Idx>&) to return the quitient generator to represent the result. See ComputeBisimulation(const Generator&, std::map<Idx,Idx>).
Definition at line 1289 of file cfl_bisimulation.cpp. ◆ ComputeNextScc()
Compute next SCC. This function provides an API for the iterative computation of SCCs. It invokes SearchScc() to find the next SCC and then adds the SCC to the StatesAvoid Filter. This approach is not computationally efficient but it allows for simple Lua wrappers.
Definition at line 560 of file cfl_graphfncts.cpp. ◆ ComputeScc() [1/4]
Compute strongly connected component (SCC) This function is a API wrapper that calls the recursive implementation SearchScc(). It internally edits the filter to require the specified initial state and to stop on the first SCC found. In particular, any other state requirement will be ignored.
Definition at line 407 of file cfl_graphfncts.cpp. ◆ ComputeScc() [2/4]
Compute one strongly connected component (SCC) This functions searchs for the first SCC of the generator rGen while applying the filter rFilter; see SCCFilter for details. Technically, this function is a API wrapper that calls the recursive implementation SearchScc() as presented in – Aho, Hopcroft, Ullman: The Design and Analysis of Computer Algorithms –
Definition at line 463 of file cfl_graphfncts.cpp. ◆ ComputeScc() [3/4]
Compute strongly connected components (SCC) This function is a API wrapper that calls the recursive implementation SearchScc().
Definition at line 347 of file cfl_graphfncts.cpp. ◆ ComputeScc() [4/4]
Compute strongly connected components (SCC) This function is a API wrapper that calls the recursive implementation SearchScc().
Definition at line 391 of file cfl_graphfncts.cpp. ◆ ConflictEquivalentAbstraction()
Conflict equivalent abstraction. Two generators are conflict equivalent w.r.t. a set of silent events, if, for any test generator defined over the not-silent events, either both or non are conflicting. This functions implements a selection of conflict equivalent transformations proposed by R. Malik and H. Flordal in "Compositional verification in supervisory control", SIAM Journal of Control and Optimization, 2009. The current implementation is experimental with code based on Michael Meyer's BSc Thesis.
Definition at line 611 of file cfl_conflequiv.cpp. ◆ Deterministic()
Make generator deterministic. Constructs a deterministic generator while preserving the generated and marked languages. The implementation is based on the so called multiway merge variant of subset construction, in which the new state set becomes a subset of the power set og the given state set. It is of exponential complexity. For details on the multiway merge algorithm see "Ted Leslie, Efficient Approaches to Subset Construction, Computer Science, University of Waterloo, 1995". See also Deterministic(const Generator&,std::map<Idx,StateSet>&,Generator& rResGen) and Deterministic(const Generator&,std::vector<StateSet>&,std::vector<Idx>&,Generator& rResGen). Technical detail: if the input has no initial state, then so has the output.
Example:
Definition at line 68 of file cfl_determin.cpp. ◆ EmptyLanguage()
Empty language Lm(G)={}. Construct generator and marking the empty language, that is Lm(G)={}. Method: this function creates a deterministic generator with one initial state that is not marked. The alphabet is set as specified. No restrictions on parameters.
Definition at line 789 of file cfl_regular.cpp. ◆ EmptyLanguageIntersection()
Test for empty language intersection (same as Disjoind()). This function checks if the intersection of two languages marked by two generators is empty that is the two languages are disjoint. The involved generated (prefix-closed) languages are not considered. This function is identical to Disjoint(). No restrictions on parameters.
Definition at line 227 of file cfl_regular.cpp. ◆ EmptyStringLanguage()
Empty string language, L(G)=Lm(G)={epsilon}. Construct generator generating and marking the empty string, that is L(G)=Lm(G)={epsilon}. Method: this function creates a generator with one marked init state and the alphabet rAlphabet. No restrictions on parameters.
Example:
Definition at line 760 of file cfl_regular.cpp. ◆ FullLanguage()
Full Language, L(G)=Lm(G)=Sigma*. Construct generator generating and marking full language Sigma* from alphabet Sigma. Method: this function creates a generator with one state that is marked and init state. This state is selflooped with all events from rAlphabet.
Example:
Definition at line 684 of file cfl_regular.cpp. ◆ HasScc()
Test for strongly connected components (SCC) This functions searchs for the first SCC of the generator rGen while applying the filter rFilter; see SCCFilter for details. Technically, this function is an API wrapper that calls the recursive implementation SearchScc() as presented in – Aho, Hopcroft, Ullman: The Design and Analysis of Computer Algorithms –
Definition at line 514 of file cfl_graphfncts.cpp. ◆ InvProject()
Inverse projection. This adds selfloop transition at every state for all missing events.
Definition at line 1479 of file cfl_project.cpp. ◆ IsAccessible()
RTI wrapper function. See also vGenerator::IsAccessible(). Definition at line 3879 of file cfl_generator.cpp. ◆ IsCoaccessible()
RTI wrapper function. See also vGenerator::IsCoaccessible(). Definition at line 3884 of file cfl_generator.cpp. ◆ IsComplete() [1/2]
RTI wrapper function. See also vGenerator::IsComplete(). Definition at line 3899 of file cfl_generator.cpp. ◆ IsComplete() [2/2]
RTI wrapper function. See also vGenerator::IsComplete(). Definition at line 3909 of file cfl_generator.cpp. ◆ IsDeterministic()
RTI wrapper function. See also vGenerator::IsDeterministic(). Definition at line 3914 of file cfl_generator.cpp. ◆ IsEmptyLanguage()
Test for Empty language Lm(G)=={}. Tests if the language marked by rGen is empty, that is if Lm(G)=={}. The generated language L(G) is not considered. Method: This function tests if a) the set of marked states is empty or else b) the intersection of the set of accessible states and the set of marked states is empty, i.e. if there is no marked state or if no marked state is accessible (reachable). No restrictions on parameter.
Definition at line 806 of file cfl_regular.cpp. ◆ IsNonblocking() [1/2]
Test for nonblocking generator. A generator G is nonblocking if closure(Lm(G)) = L(G), i.e. if every accessible state is coacessile. The specified generator must be deterministic.
Definition at line 980 of file cfl_regular.cpp. ◆ IsNonblocking() [2/2]
Test for nonblocking marked languages. Two languages L1 and L2 are nonblocking, if closure(L1 || L2) == closure(L1) || closure(L2). This function performs the parallel composition of the two specified generators and tests it for nonblockingness. Provided that both generators are trim, this is equivalent to the respective marked languages being nonblocking. The specified generators must be trim.
Definition at line 988 of file cfl_regular.cpp. ◆ IsNonconflicting()
Test for conflicts. A family of generators is non-blocking, if their parallel composition is non-blocking (all accessible states are co-accessible). This implementation applies a number of conflict equivalent simplifications before finally testing for conflicts in the parallel composition; This approach has been originally proposed by R. Malik and H. Flordal in "Compositional verification in supervisory control", SIAM Journal of Control and Optimization, 2009. The current implementation is based on Michael Meyer's BSc Thesis and repaired/optimized by Yiheng Tang
Definition at line 618 of file cfl_conflequiv.cpp. ◆ IsOmegaClosed()
Test for topologically closed omega language. This function tests whether the omega language Bm(G) realized by the specified generator G is topologically closed. Method: First, compute the omega-trim state set and restrict the discussion to that set. Then, omega-closedness is equivalent to the non-existence on a non-trivial SCC with no marked states.
Definition at line 488 of file cfl_omega.cpp. ◆ IsOmegaTrim()
RTI wrapper function. See also vGenerator::IsOmegaTrim(). Definition at line 3894 of file cfl_generator.cpp. ◆ IsPrefixClosed()
Test for prefix closed marked language. This function tests whether the language Lm(G) marked by the specified generator G is prefix closed. It does so by testing whether all accessible and coaccessible states are marked. The specified generator must be deterministic.
Definition at line 969 of file cfl_regular.cpp. ◆ IsStronglyCoaccessible()
RTI wrapper function. See also MtcSystem::IsStronglyCoaccessible(). Definition at line 32 of file mtc_generator.cpp. ◆ IsStronglyTrim()
RTI wrapper function. See also MtcSystem::IsStronglyTrim(). Definition at line 37 of file mtc_generator.cpp. ◆ IsTrim()
RTI wrapper function. See also vGenerator::IsTrim(). Definition at line 3889 of file cfl_generator.cpp. ◆ KleeneClosure() [1/2]
Kleene Closure. This function is a convenience wrapper for KleeneClosure(Generator&). Definition at line 861 of file cfl_regular.cpp. ◆ KleeneClosure() [2/2]
Kleene Closure. This function computes the Kleene Closure ( ()* - operator) of the language marked by rGen. The generated language is not considered. Method: KleeneClosureNonDet() is called, which, for all transitions leading from a state x to a marked state, inserts a transition with the same event starting from x and leading to (one of) the initial state(s). As this step causes nondeterminism, the function Deterministic() is called. See also KleeneClosureNonDet(). No restrictions on parameter.
Example:
Definition at line 838 of file cfl_regular.cpp. ◆ KleeneClosureNonDet()
Kleene Closure, nondeterministic version. This function computes the Kleene Closure ( ()* - operator) of the language marked by rGen. The generated language is not considered. Method: KleeneClosureNonDet() is called, which, for all transitions leading from a state x to a marked state, inserts a transition with the same event starting from x and leading to (one of) the initial state(s).
Definition at line 892 of file cfl_regular.cpp. ◆ LanguageComplement() [1/4]
Language Complement (uniform API wrapper).
Definition at line 498 of file cfl_regular.cpp. ◆ LanguageComplement() [2/4]
Language Complement (uniform API wrapper).
Definition at line 491 of file cfl_regular.cpp. ◆ LanguageComplement() [3/4]
Language complement. Convert generator marking the language Lm into generator marking the language complement of Lm which is defined as Sigma*-Lm. In this function, Sigma is given by the alphabet of rGen; see also LanguageComplement(rGen,rAlphabet). The original generated language is ignored. Method: This function calls Automaton() first and then inverts the marking of the states of the result. Determinism: Input parameter has to be deterministic for correct result, see Automaton() for explanations. If FAUDES_CHECKED is defined a warning on non-deterministic input is issued. (by function Automaton()). No further restrictions on parameter.
Example:
Definition at line 482 of file cfl_regular.cpp. ◆ LanguageComplement() [4/4]
Language complement wrt specified alphabet. Convert generator marking the language Lm into generator marking the language complement of Lm which is defined as Sigma*-Lm. In this function, Sigma is given by the parameter rAlphabet. The original generated language is ignored. Method: This function calls Automaton() first and then inverts the marking of the states of the result. Determinism: Input parameter has to be deterministic for correct result, see Automaton() for explanations. If FAUDES_CHECKED is defined a warning on non-deterministic input is issued. (by function Automaton()). No further restrictions on parameter.
Definition at line 462 of file cfl_regular.cpp. ◆ LanguageConcatenate()
Language concatenation, deterministic version. With the languages Lm1 and Lm2 marked by rGen1 and rGen2, respectively, the result rResGen marks the concatenation LmRes=Lm1Lm2. The languages generated by rGen1 and rGen2 are ignored. It would be possible to let the result also generate the concatenation of the generated languages; however, this can produce disproportionate computational overhead, if only the marked languages shall be concatenated. Method: rGen2 is appended to rGen1: first, the initial states of rGen2 are erased. Then, transitions, that formerly started from the initial state(s) of rGen2, are redirected and multiplied such that they start from each marked state of rGen1. The marked states corresponding to rGen2 remain marked. The marked states of rGen1 remain marked only if rGen2 has at least one marked initial state (i.e. if epsilon is concatenated to Lm1.) Determinism: Input parameters may be nondeterministic. This function calls LanguageUnionNonDet() and then Deterministic() to convert the result into a deterministic generator. Note that this conversion is usually straightforward, but there exist theoretical worst-case examples of exponential complexity. No restrictions on parameters.
Example:
Definition at line 663 of file cfl_regular.cpp. ◆ LanguageConcatenateNonDet()
Language concatenation, nondeterministic version. With the languages Lm1 and Lm2 marked by rGen1 and rGen2, respectively, the result rResGen marks the concatenation LmRes=Lm1Lm2. The languages generated by rGen1 and rGen2 are ignored. It would be possible to let the result also generate the concatenation of the generated languages; however, this can produce disproportionate computational overhead, if only the marked languages shall be concatenated. Method: rGen2 is appended to rGen1: first, the initial states of rGen2 are erased. Then, transitions, that formerly started from the initial state(s) of rGen2, are redirected and multiplied such that they start from each marked state of rGen1. The marked states corresponding to rGen2 remain marked. The marked states of rGen1 remain marked only if rGen2 has at least one marked initial state (i.e. if epsilon is concatenated to Lm1.) Determinism: Input parameters may be nondeterministic. Result can be nondeterministic even if input parameters are deterministic; see also LanguageConcatenate(). No restrictions on parameters.
Definition at line 559 of file cfl_regular.cpp. ◆ LanguageDifference()
Language difference (set-theoretic difference). This function calculates Lm1-Lm2 (sometimes also denoted by Lm1\Lm2), that is the set of all strings included in Lm1 but not in Lm2. Method: The language difference is computed by taking the intersection of Lm1 with the complement of Lm2. Determinism: Due to the use of LanguageComplement(), rGen2 has to be deterministic. Result can be nondeterministic only if rGen1 is nondeterministic. Restrictions on prameters: rGen2 has to be deterministic.
Example:
Definition at line 507 of file cfl_regular.cpp. ◆ LanguageDisjoint()
Test whether two languages are disjoint. This function tests whether the intersection of two languages marked by two generators is empty, ie the two languages are disjoint. The involved generated (prefix-closed) languages are not considered. This function is identical to EmptyLanguageIntersection(). No restrictions on parameters.
Definition at line 332 of file cfl_regular.cpp. ◆ LanguageEquality()
Language equality, Lm1==Lm2. Test if the language Lm1 marked by rGen1 equals the language Lm2 marked by rGen2. The generated languages are not considered. Method: This function checks mutual inclusion of Lm1 in Lm2 and of Lm2 in Lm1 using the function LanguageInclusion(). Restrictions on parameters: rGen1 and rGen2 have to be deterministic! If FAUDES_CHECKED is defined a warning on non-deterministic input is issued. (by function Automaton()). ToDo: implement faster, version using a variant of Product(): compute product without storing result, return false as soon as rGen1 and rGen2 "disagree" on the occurrence of some event.
Definition at line 829 of file cfl_regular.cpp. ◆ LanguageInclusion()
Test language inclusion, Lm1<=Lm2. Test if language Lm1 marked by rGen1 is included in language Lm2 marked by rGen2. The generated languages are not considered. Method: This function checks if there is no string in Lm1 that is not in Lm2 by testing if the intersection of Lm1 and the language complement of Lm2 is empty. Restrictions on parameters: rGen2 has to be deterministic! If FAUDES_CHECKED is defined a warning on non-deterministic input is issued. (by function Automaton()). Determinism: correctness in case of nondeterministic parameter rGen1 has been tested with an example (see ExInclusion_simple), but not proven. ToDo: implement faster version using a variant of Product(): compute product without storing result, return false as soon as some event is possible in Lm2 but not in Lm1.
Definition at line 815 of file cfl_regular.cpp. ◆ LanguageIntersection()
Language intersection. This function performs the intersection of two languages marked by two generators; the resulting generator marks the resulting language. Moreover, the same is done for the involved generated (prefix-closed) languages. The resulting languages are defined over the intersection of the involved alphabets. Method: This function calls Product(). In the product of two automata, an event occurs if and only if it occurs in both automata rGen1 and rGen2. The result generates/marks the intersection of the involved languages, see e.g. [Cassandras, Lafortune. Introduction to Discrete Event Systems, p.84] Determinism: Input parameters may be nondeterministic. Result can be nondeterministic only if input parameters are nondeterministic. No restrictions on parameters.
Example:
Definition at line 188 of file cfl_regular.cpp. ◆ LanguageUnion()
Language union, deterministic version. This function performs the union of two languages marked by two generators; the resulting generator marks the resulting language. Moreover, the same is done for the involved generated (prefix-closed) |languages. Method: This function implements the textbook version (which textbook??) in taking unions of all generator entities (alphabets, initial states, ...). State sets are taken as disjoint by definition and thus reindexed and renamed to achieve disjoint union. The resulting language is defined over the union of the alphabets of the original languages. Determinism: Input parameters may be nondeterministic. This function calls LanguageUnionNonDet() and then Deterministic() to convert the result into a deterministic generator. Note that this conversion is usually straightforward, but there exist theoretical worst-case examples of exponential complexity. No restrictions on parameters. ToDo: a version similar to parallel composition that produces a deterministic result by construction. (?)
Example:
Definition at line 127 of file cfl_regular.cpp. ◆ LanguageUnionNonDet()
Language union, nondeterministic version. This function performs the union of two languages marked by two generators; the resulting generator marks the resulting language. Moreover, the same is done for the involved generated (prefix-closed) languages. Method: This function implements the textbook version in taking unions of all generator entities (alphabets, initial states, ...) of rGen1 and rGen2. State sets are taken as disjoint by definition and thus reindexed and renamed to achieve disjoint union. The resulting language is defined over the union of the alphabets of the original languages; original languages defined over different alphabets are treated as if they were defined over the union of both alphabets. Determinism: Input parameters may be nondeterministic. This function is more economical than the deterministic version, but likely to produce a non-deterministic result; see also LanguageUnion(). No restrictions on parameters.
Definition at line 45 of file cfl_regular.cpp. ◆ MarkAllStates()
RTI wrapper function. Definition at line 3986 of file cfl_generator.cpp. ◆ OmegaClosure()
Topological closure. This function computes the topological closure the omega language Bm realized by rGen. Method: First, OmegaTrim is called to erase all states of rGen that do not contribute to Bm. Then, all remaining states are marked. No restrictions on parameter.
Example:
Definition at line 470 of file cfl_omega.cpp. ◆ OmegaParallel()
Parallel composition with relaxed acceptance condition. This version of the parallel composition relaxes the synchronisation of the acceptance condition (marking). It requires that the omega extension of the generated language has infinitely many prefixes that comply to the marked languages of G1 and G2, referring to the projection on the respective alphabet. It does however not require the synchronous acceptance.
Definition at line 261 of file cfl_omega.cpp. ◆ OmegaProduct()
Product composition for Buechi automata. Referring to the Buechi acceptance condition, the resulting genarator accepts all those inifinite words that are accepted by both, G1 and G2. This implementation extends the usual product state space by a flag to indentify executions with alternating marking.
Definition at line 102 of file cfl_omega.cpp. ◆ OmegaTrim() [1/2]
RTI wrapper function. See also vGenerator::OmegaTrim(). Definition at line 3980 of file cfl_generator.cpp. ◆ OmegaTrim() [2/2]
RTI wrapper function. See also vGenerator::OmegaTrim(). Definition at line 3975 of file cfl_generator.cpp. ◆ Parallel() [1/2]
Parallel composition. Constructs the parallel composition of two generators, where shared events are synchronised while non-shared events are executed independantly. The resulting generators alphabet is the union of the argument alphabets. In this implementation, only accessible states are generated. On deterministic input this functions constructs a deterministic output. See also Parallel(const Generator&,std::map< std::pair<Idx,Idx>, Idx>&,const Generator&, Generator&).
Example:
Definition at line 32 of file cfl_parallel.cpp. ◆ Parallel() [2/2]
Parallel composition. See also Parallel(const Generator&, const Generator&, Generator&). This version fills a composition map to map pairs of old states to new states.
Definition at line 159 of file cfl_parallel.cpp. ◆ PrefixClosure()
Prefix Closure. This function computes the prefix closure the language Lm marked by rGen. A language Lm is prefix closed if each string of Lm implies that all its prefixes are also element of Lm. The prefix closure of a language marked by a generator is always a subset of the generated language and is represented by the set of coaccessible states of the generator. Method: First, Coaccessible() is called to erase all states of rGen that do not represent prefixes of marked strings. Then, all remaining states are marked. No restrictions on parameter. ToDo: (slightly) more efficient version: implement generator function CoAccessibleSet() similar to AccessibleSet() and call InjectMarkedStates(AccessibleSet()).
Example:
Definition at line 950 of file cfl_regular.cpp. ◆ Product()
Product composition. The product composition executes shared events only. The resulting generators alphabet is the interscetion of the argument alphabets. In this implementation, only accessible states are generated. Assumes deterministic input generators, result is deterministic.
Definition at line 418 of file cfl_parallel.cpp. ◆ Project()
Deterministic projection. Projects the generated and marked languages to a subalphabet of the original alphabet, and subsequently calls Deterministic to construct a deterministic realisation of the result. The input generator does not need to be deterministic.
Example:
Definition at line 1349 of file cfl_project.cpp. ◆ ProjectNonDet()
Language projection. Projects the generated and marked languages to another alphabet. Transitions with events not in the projection alphabet are considered invisible and therefor acordingly relinked with a visible lable to the appropriate successor state. The projection alphabet is intended (but not required) to be a subset of the original alphabet. The default implementation is based on a local forward reachability analysis per state. It known to suffer from performance issues for certain large automata. This was in particular the case for the variation used in libFAUDES 2.14 up to 2.23. A number of alternatives are now available in "cfl_project.cpp" and can bet set as the default by adjusting the respective wrapper function (grep for "wrapper" in "cfl_project.cpp"). If you experience trouble with the current revision, you can set the default to revert to pre libFAUDES 2.24 behaviour – and please report back to us. The candidate for future releases is available for testing, see ProjectNonDetScc(Generator&, const EventSet&). The results in general is nondeterministic. The input generator does not need to be deterministic. See Project(const Generator&,const EventSet&, Generator&) for a version with deterministic result.
Definition at line 1334 of file cfl_project.cpp. ◆ ProjectNonDetScc()
Language projection. Projects the generated and marked languages to another alphabet, see also ProjectNonDetScc(Generator&, const EventSet&). This implementation first eliminates silent strongly connected components and then applies a local backward reachability analysis. Performance benefits are significant for certain large generators. The input generator does not need to be deterministic. The results in general is nondeterministic. You may manually invoke Deterministic() to convert the result.
Definition at line 1343 of file cfl_project.cpp. ◆ SelfLoop() [1/2]
Self-loop all states. This function selfoops all states of rGen with the events from rAlphabet. Method: The alphabet of rGen is extended by rAlphabet. For each state x of rGen and each event alpha of rAlphabet, a transition (x,alpha,x) is inserted, irrespective of whether this event was already active in x before. See also SelfLoop(rGen,rAlphabet,rStates) and SelfLoopMarkedStates(rGen,rAlphabet). No restrictions on parameter. Determinism: resulting generator is nondeterministic, if it was nondeterministic before, or if rGen already contains one or more (non selfloop) transitions with events from rAlphabet.
Example:
Definition at line 1003 of file cfl_regular.cpp. ◆ SelfLoop() [2/2]
Self-loop specified states. This function selfoops the states rStates of rGen with the events from rAlphabet. Method: The alphabet of rGen is extended by rAlphabet. For each state x of rStates and each event alpha of rAlphabet, a transition (x,alpha,x) is inserted, irrespective of whether this event was already active in x before. See also SelfLoop(rGen,rAlphabet) and SelfLoopMarkedStates(rGen,rAlphabet). No restrictions on parameter. Determinism: resulting generator is nondeterministic, if it was nondeterministic before, or if rGen already contains one or more (non selfloop) transitions starting from a state of rState with events from rAlphabet.
Example:
Definition at line 1059 of file cfl_regular.cpp. ◆ SelfLoopMarkedStates()
Self-loop all marked states. This function selfoops all marked states of rGen with the events from rAlphabet. Method: The alphabet of rGen is extended by rAlphabet. For each marked state x of rGen and each event alpha of rAlphabet, a transition (x,alpha,x) is inserted, irrespective of whether this event was already active in x before. See also SelfLoop(rGen,rAlphabet) and SelfLoop(rGen,rAlphabet,rStates). No restrictions on parameter. Determinism: resulting generator is nondeterministic, if it was nondeterministic before, or if rGen already contains one or more (non selfloop) transitions starting from a marked state with events from rAlphabet.
Example:
Definition at line 1030 of file cfl_regular.cpp. ◆ StateMin()
State set minimization. Constructs a generator with minimal stateset while preserving the generated und marked languages. This function implements the (n*log n) set partitioning algorithm by John E. Hopcroft. The algorithm expects an accessible input generator. To have a const interface, the argument is copied. See also StateMin(Generator&,Generator&).
Example:
Definition at line 613 of file cfl_statemin.cpp. ◆ StronglyCoaccessible() [1/2]
RTI wrapper function. See also MtcSystem::Coaccessible(). Definition at line 47 of file mtc_generator.cpp. ◆ StronglyCoaccessible() [2/2]
RTI wrapper function. See also MtcSystem::Coaccessible(). Definition at line 42 of file mtc_generator.cpp. ◆ StronglyTrim() [1/2]
◆ StronglyTrim() [2/2]
◆ Trim() [1/2]
RTI wrapper function. See also vGenerator::Trim(). Definition at line 3969 of file cfl_generator.cpp. ◆ Trim() [2/2]
RTI wrapper function. See also vGenerator::Trim(). Definition at line 3964 of file cfl_generator.cpp. ◆ UniqueInit() [1/2]
Make initial states unique. Convenience wrapper for UniqueInit(Generator&).
Definition at line 62 of file cfl_determin.cpp. ◆ UniqueInit() [2/2]
Make initial states unique. If the argument generator has precisely one initial state, this function does nothing. Else, this function introduces a new and unique initial state and relinks transitions accordinly. If the argument generator used to have more than one initial state, this operation may render the output nondeterministic. If the argument generator used to have no initial state, the output generator will generate the empty string language as opposed to the empty language. Otherwise, generated and marked languages are preserved. Note: call this function followed by determine to convert the generator to a deterministic generator with exactly one initial state.
Definition at line 28 of file cfl_determin.cpp. libFAUDES 2.32b --- 2024.03.01 --- c++ api documentaion by doxygen |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
