• libFAUDES
• Reference  
• Type Index  
• Function Index  
• Literature  
•  
• Sections
• CoreFaudes  
  • CoreFaudes
  • Introduction
  • Generators
  • Alphabets
  • Reachability
  • Boolean Operations
  • Regular Expressions
  • Synchronous Composition
  • Projection
  • StateSet Conversion
  • Elementary Types
  • Miscellaneous
  • Vector Types
• CoordinationControl  
• Diagnosis  
  • Diagnosis
  • Introduction
  • Event-Diagnosis
  • Language-Diagnosis
  • Modular Diagnosis
  • Decentralized Diagnosis
  • Application Example
• FaultTolerantControl  
  • FaultTolerantControl
  • Introduction
  • Example
  • Fault-Accommodation
  • Reconfiguration
  • Fault-Patterns
• HioSys  
  • HioSys
  • Introduction
  • Step-By-Step
  • Synthesis Procedure
  • Liveness Properties
  • Application Example
• IoSystem  
  • IoSystem
  • Introduction
  • Properties
  • Synthesis
• Multitasking  
  • Multitasking
  • Introduction
  • Functions
  • Observer
  • Optimal Color Set
  • Reachability
  • Synthesis
• Observer  
  • Observer
  • Introduction
  • Verification
  • Synthesis
  • Example
• OmegaAut  
  • OmegaAut
  • Introduction
  • Buechi-Functions
  • Buechi-Control
• Priorities  
• Simulator  
  • Simulator
  • Introduction
  • Executor Classes
  • Hardware-In-The-Loop
  • IO-Devices
  • Simulator Interconnection
• Synthesis  
  • Synthesis
  • Introduction
  • Controllability
  • Normality
  • Completeness
  • Misc Functions
•  
• Functions
• BuechiClosure  
• BuechiCon  
• BuechiConNorm  
• BuechiParallel  
• BuechiProduct  
• BuechiTrim  
• IsBuechiClosed  
• IsBuechiControllable  
• IsBuechiRelativelyClosed  
• IsBuechiTrim  
• SupBuechiCon  
• SupBuechiConNorm  
•  

Synthesis w.r.t. Buechi Acceptance

Functions related to controllability and controller synthesis for non-terminating processes realised by Buechi automata.

Definition of Omega-Controllability

Addressing the control of discrete-event systems on the infinite time axis, [W2] develops the following notion of omega-controllability.

Consider two omega languages L and K over a common alphabet Sigma, and a set of uncontrollable events Sigma_uc ⊆ Sigma. Then K is said to be omega-controllable w.r.t (L,Sigma_uc) if the following conditions are satisfied:

(i)  Prefix(K) is controllable w.r.t (Prefix(L),Sigma_uc), i.e., Prefix(K)Sigma_uc ∩ Prefix(L)  ⊆  Prefix(K) ; and
(ii)  K is relatively topological closed w.r.t. L, i.e., K  =  Closure(K) ∩ L .

Note 1: for omega-languages, the closure operator Closure(.) refers to the so called topological closure; see also BuechiClosure. The prefix operator Prefix(.) gives the set of all finite length prefixes.

Note 2: The above definition of omega-controllability conforms to [W2] and [W3]. It must not be confused with the more general approach taken in [W4]; see also SupBuechiCon.

Note 3: all omega-languages in the following discussion are assumed to be representable by finite deterministic automata with Buechi acceptance condition. Given a finite deterministic generator G, we write Bm(G) for the associated omega-language and obtain Bm(G) = B(Lm(G)) by determinism of G; see also Buechi acceptance condition.

Controller Synthesis for Omega-Languages

Consider two omega languages L and E over a common alphabet Sigma to represent the plant and the specification, respectively. Let Sigma_uc ⊆ Sigma denote the set of uncontrollable events. The task then is to find a topologically closed controller H ⊆ Sigma^w, such that

(1)     L and H are non-blocking, i.e., Prefix(L ∩ H) = Prefix(L) ∩ Prefix(H) ;
(2)     the controller H exhibits a prefix which is controllable w.r.t. (Prefix(L),Sigma_uc) ; and,
(3)     the closed-loop behaviour satisfies the specification, i.e., L ∩ H ⊆ E.

For any topologically closed controller H which satisfies the above conditions, the closed loop K = L ∩ H exhibits the following properties:

(a)     K is relatively topological closed w.r.t. L; and,
(b)     Prefix(K) is controllable w.r.t. (Prefix(L),Sigma_uc); and,
(c)     K ⊆ E.

Note that (a) and (b) amount to omega-controllability. Moreover, if a language K satisfies (a)-(c), the controller H = Closure(K) solves the synthesis problem.

In contrast to the situation of star-languages, property (a) is in general not retained under arbitrary union. Thus, the supremum

K↑ := sup{ K ⊆ E | K is omega-controllable w.r.t (L,Sigma_uc) }

may fail to be an achievable closed-loop behaviour and the controller H↑ = Closure(K↑) may fail to enforce the specification. As a consequence of this observation, the synthesis problem disintegrates in two distinct cases.

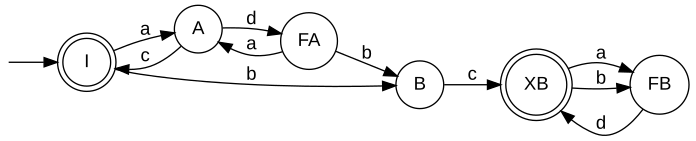
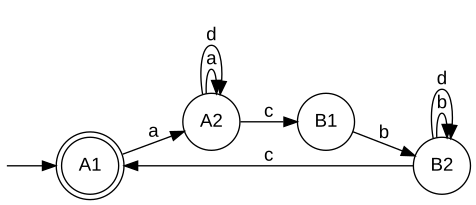
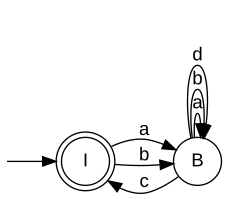
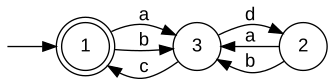
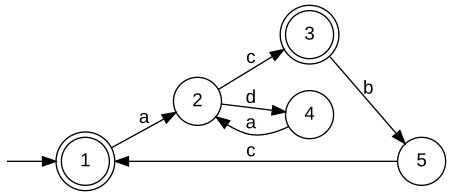
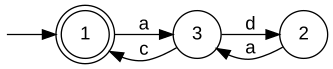
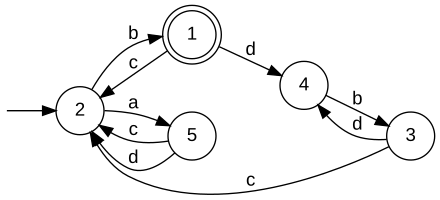
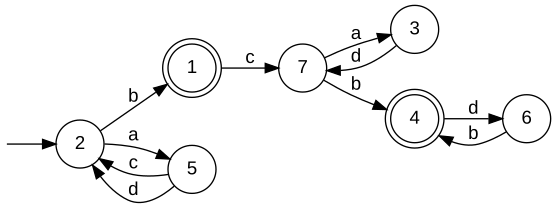
Relatively closed specifications

Under the additional hypothesis, that E is relatively topological closed w.r.t. L, [W2] establishes that the supremum K↑ is indeed also relatively topological closed w.r.t. L, and, hence, is omega-controllable. For this case, [W3] discusses computational procedures which are very similar to the situation of star languages.

For a practical solution of the control problem under the given hypothesis the Synthesis Plug-In provides the function SupConCmpl. Given realisations GSpec' and Gplant with Bm(GSpec') = Closure(E) and Bm(Gplant) = L, respectively, SupConCmpl constructs a realisation GSup of K↑, i.e., K↑ = B(GSup).

When all parameters are closed, the situation further simplifies. Given realisationsn GSpec and Gplant with B(GSpec) = E and B(Gplant) = L, respectively, SupConCmplClosed constructs a realisation GSup of K↑, i.e.,K↑ = Bm(GSup).

Not-necessarily relatively closed specifications

A more general approach, that drops the requirement of the specification E to be relatively closed w.r.t. the plant L is presented in [W4]. In this situation, K↑ will fail to be relatively closed, and a controller H↑ = Closure(K↑) will fail to enforce the specification. However, one could then use K↑ itself as a supervisor, provided that a technical realisation implements a mechanism that ensures that closed-loop trajectories fulfill the acceptance condition of K↑. Alternatively, one can extract a non-minimal restrictive supervisor that can be implemented by a closed behaviour. A generator that realises K↑ can be computed by SupBuechiCon, see also the example discussed below.

Example

For illustration of omega-controllability, consider the below veriants of a machine that may run one of two processes A and B. The processes are initiated by the controllable events a and b, respectively. Once started, a process may terminate with success c or failure d. In the first variant, each process is guaranteed to eventually succeed. In the second variant, process B exhausts the machine and can subsequently only succeed after running process A. In the third variant, process B breaks the machine. Each variant exhibits an eventuality property and, hence, neither of the induced omega-languages are topologically closed.

A-B-machine, std. variant

A-B-machine, B exhausts the machine

A-B-machine, B breaks the machine

In our discussion, we consider three alternative specifications, that require the closed loop to

• persistenly alternate successful operation of processes A and B, or to
  

• persistently run some operation successfully, or to
  

• start with process A, eventually switch to B, and, on success turn back to A.
  

Note that, technically, a specification language is required to be a subset of the plant language. The above realisations are "lazy" in the sense that they do not fulfil this requirement. For the following diccussion, we think of the above specifications to be intersected with the respective plant language; see also BuechiParallel.

For a minimal restrictive supervisor to exist, the specification is required to be relatively closed w.r.t. the plant. Intuitively, this is true whenever any eventuality property required by the specification is implied by the plant. The following table comments on relative closedness of indivual combinations of plant and specification.

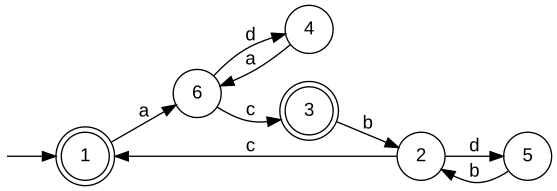
The third row of the above table points out that there are relevant applications that do not fulfil the requirement of a relatively closed specification. This has been addressed in [W4]; see also below the documentation of SupBuechiCon.

For the cases where relative closedness is satisfied, the minimal restrictive closed-loop behaviour has been computed using SupConCmpl from the Syntheis Plug-In.

A-B-machine, std. variant, with alternate-A-and-B-success specification

A-B-machine, std. variant, with persistently-any-success specification

A-B-machine, B exhausts the machine, with alternate-A-and-B-success specification

A-B-machine, B breaks the machine, with persistenly-any-success specification

SupBuechiCon

OmegaAut for omega-languages.

Signature:

SupBuechiCon(+In+ System GPlant, +In+ Generator GSpec, +Out+ Generator GSupervisor)

SupBuechiCon(+In+ Generator GPlant, +In+ EventSet AContr, +In+ Generator GSpec, +Out+ Generator GSupervisor)

Detailed description:

The function SupBuechiCon addresss the situation where the specification fails to be relatively closed w.r.t. the plant. We formaly model the closed-loop interconnection of a plant L ⊆ Sigma^w and supervisor K ⊆ L by the intersection L∩K. Since we dropped the requirement of relative closedness, we obtain

L ∩ K  =  K  ⊆  L ∩ Closure(K).

We require the closed-loop to be nonblocking and the supervisor not to disable uncontrollable events, i.e. for all s ∈ Prefix(L) ∩ Prefix(K) we must have

(a)   s ∈ Prefix(L∩K) and
(b)   o ∈ Sigma_uc, so ∈ Prefix(L)    ⇒    so ∈ Prefix(K) .

The nonblockng condition (a) is trivially fulfilled, while (b) amounts to controllabiliy for the prefix of K w.r.t. the prefix of L. Neither for the plant nor for the supervisor we ask how a technical realization actually manages to satisfy their respective acceptance condition. However, while K ⊆ L ensures that the supervisor will support the plant in this regard, the plant could permanently prevent the supervisor from running into a marked state. Thus, we introcude as condition (c) that while the closed-loop evolves, the supervisor must allways have the chance to apply a control strategy such that the acceptance condition of the plant implies that the trajectory eventually passes a maked state. Technically, we require for all s ∈ Prefix(L) ∩ Prefix(K)

(c)    ∃ V ⊆ K: s ∈ Prefix(V), and V is omega-controllable w.r.t. L.

It is readily verified that condition (c) implies condition (b). Furthermore, all three conditions are preserved under arbitrary union. Thus, given a specification E ⊆ L, there exists a supremal closed-loop behaviour K ⊆ E that satisfies conditions (a), (b) and (c). Moreover, supremal closed-loop behaviour equals the union over all omega-controllable sublanguages of E.

Note. A more general approach to the control of omega-languages has been developed in [W4]. When applied to the specific case of determinitsic Buchi automata addressed here -- and despite some minor differences in the perspective we take -- the above condition (c) is equivalent to the notion of omega-controllability proposed in [W4]. There, it has been shown that the supremal controllable sublanguage can be represented in terms of the so called controllability prefix and the marking of the specification. The current of implementation SupBuechiCon is derived as an adaption of the methods proposed in [W4] (and companion papers) to the specific case at hand.

Example:

The following results have been obtained for the three variants of A-B-machine and the eventually-switch-to-B specification.

A-B-machine, std. variant, with eventually-switch-to-B specification

A-B-machine, B exhausts the machine, with eventually-switch-to-B specification

A-B-machine, B breaks the machine, eventually-switch-to-B specification

Parameter Conditions:

This implementation requires the alphabets of plant and specification to match. Furthermore, both generators must be deterministic. Effectively, the specification is intersected with the plant. The result will be deterministic and omega-trim.

libFAUDES 2.33h --- 2025.06.17 --- with "synthesis-omegaaut-observer-diagnosis-iosystem-hiosys-multitasking-coordinationcontrol-timed-iodevice-priorities-simulator-luabindings"