Language-Diagnosis.

We consider language-diagnosability as employed in [D3], [D4], [D5]. Given a generator G and a set of observable events Sigma0, a specification language K characterize faulty behavior. A failure occurs as soon as a string in the plant G is not an element of the specification language K.

Language-Diagnosability requires that every deviation from the behavior specified by K has to be detected after the occurrence of a finite number of events. In the diagnoser plug-in, language-diagnosability is verified with the function IsLanguageDiagnosable. In addition, the function LanguageDiagnoser computes a Diagnoser such that -- in the presence of language-diagnosability -- any deviation from the specified behavior will be unambiguously detected after the occurrence of a finite number of events.

LanguageDiagnoser

Computes event-diagnoser w.r.t. failure types.

Signature:

LanguageDiagnoser(+In+ System GArg, +In+ Generator EArg, +Out+ Diagnoser GRes)

Detailed description:

Provided that the specified generator is diagnosable, this function computes the corresponding language-diagnoser.

Based on the specification language EArg, the implementation uses basic language operations to obtain a generator Gf that marks the failure behaviour, denoted by the failure type F. A procedure similar to the one above is then used to synthesise a diagnoser. The current implementation, however, is experimental.

Parameter Conditions:

Same as with IsDiagnosable and IsLanguageDiagnosable, respectively.

IsLanguageDiagnosable

Tests for language-diagnosability w.r.t. a specification language.

Signature:

IsLanguageDiagnosable(+In+ System GArg, +In+ Generator EArg, +Out+ Boolean BRes)

Detailed description:

Given a generator G, a specification E and a set of observable events Sigma0, it is considered a failure whenever GArg evolves along a string s ∉ L(E). If any such failure can be detected within a uniformly bounded number transitions, the GArg is said to be diagnosable w.r.t (Sigma0, E).

To formally state the requirement, let H = L(G)-Lm(E) denote the set of strings that do not (yet) fulfill the specification. Language diagnosability is then defined by the condition

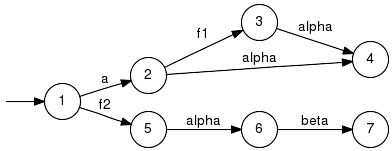
( ∃ n ) ( ∀ s ∈ H ) ( ∀ st ∈ H, |t|>n or st deadlocks )    [ Pinv0 P0(st)  ⊆ H ] .

The algorithm performs the polynomial-time language-diagnosability algorithm proposed in [D5]. Note that the current implementation does not use an additional observation mask but is based on a natural projection in order to determine the observations.

Parameter Conditions:

GArg and EArg are deterministic. The current implementation returns false if the requirements are not met.

Example

We illustrate the concept of language diagnosability and the computation of a corresponding diagnoser in the following example with the plant G that has to fulfill the apecification K.

Plant G Language specification K

In this example, diagnosability is violated. Although the faulty string f2 ∉ K can be uniquely detected after the occurrence of beta, the faulty string a f1 ∉ K cannot be resolved, since all possible extensions of a f1 have the same observation as a non-faulty string. This can also be verified by looking at the (unsuccessful) diagnoser computed with the function LanguageDiagnoser as shown below. The faulty string f2 can be diagnosed in the state with the label 7F, while all possible extensions of a f1 with the event alpha lead to the confused state with the label 4NF 6F.

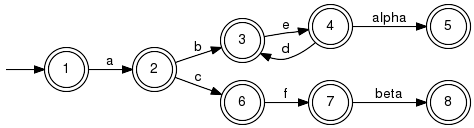
Diagnoser for the plant G and the specification K

Abstraction-based Language-Diagnosis.

In order to reduce the computational complexity of the diagnosability verification, the concept of abstraction-based language diagnosability is introduced. Here, it is assumed that the specification K is given over a subalphabet "\hat{Sigma} ⊆ Sigma" and it is proposed to use an abstraction \hat{G} of the original plant G for the diagnosability test with the function IsLanguageDiagnosable. The abstraction-based language diagnosabilty is successful if certain sufficient conditions are fulfilled. In particular, the projection of the plant language L(G) to the abstraction alphabet \hat{Sigma} has to be a loop-preserving observer as described below.

IsLoopPreservingObserver

Tests if a given projection is a loop-preserving observer.

Signature:

IsLoopPreservingObserver(+In+ System GArg, +In+ EventSet AArg, +Out+ Boolean BRes)

Detailed description:

Given a generator G and an abstraction alphabet \hat{Sigma} the projection p:Sigma*→\hat{Sigma}* is a loop-preserving observer if it is an observer (IsObs) and there are no loops in G only with events in Sigma-\hat{Sigma}.

The algorithm performs the polynomial-time observer verification in [D1] and the search algorithm for strongly connected components by Tarjan.

Parameter Conditions:

GArg has to be deterministic and \hat{Sigma} has to be a subset of Sigma. The current implementation returns false if the requirements are not met.

Example

We illustrate the concept of a loop-perserving observer and the corresponding application of IsLoopPreservingObserver by the following automaton G and the abstraction alphabet \hat{Sigma} =  {alpha, beta}.

Plant G

In this example, the loop-preserving observer condition is violated, since there is a loop with the events e and d that are not in the abstraction alphabet.

LoopPreservingObserver

Compute a loop-preserving observer from a given initial alphabet.

Signature:

LoopPreservingObserver(+In+ System GArg, +In+ EventSet IArg, +Out+ EventSet AArg)

Detailed description:

If the loop-preserving observer condition is violated, a further relevant problem is the extension of the abstraction alphabet until the loop-preserving observer condition holds.

The algorithm iteratively evaluates all possible alphabet extensions and terminates if a minimal (smallest number of events) extension is found that fulfills the loop-preserving observer condition. Note that, in the worst-case, no abstraction is possible, that is, Sigma = \hat{Sigma}.

Parameter Conditions:

GArg has to be deterministic and \hat{Sigma} has to be a subset of Sigma.

Example

Applying the function LoopPreservingObserver to the above example, the extended abstraction alphabet \hat{Sigma} = {b,c,d,e,alpha,beta} fulfills the loop-preserving observer condition.

libFAUDES 2.32b --- 2024.03.08 --- with "synthesis-observer-diagnosis-iosystem-hiosys-multitasking-coordinationcontrol-timed-iodevice-simulator-luabindings"

>>