I/O Systems Controller Synthesis

Since I/O systems refer to the inifinite time axis, conditions imposed on the closed-loop are essentially the same as for the supervision of omega-languages; see [S3], [S5]. In the context of an abstraction based design, however, the formal nonblocking property becomes nontrivial. Technically, we impose the following admissibility condition, which is closely related to omega-controllablity proposed in [S5]:

Given an alphabet Sigma = U∪Y partitioned in input events U and output events Y, and consider a plant L ⊆ Sigma^w. Then, a controller H ⊆ Sigma^w is omega-admissible w.r.t. L, if
for all s ∈ Prefix(L)∩Prefix(H) there exists a V ⊆ L∩H, s ∈ Prefix(V), such that

  • Prefix(V) is controllable w.r.t. (Prefix(L),Y), and

  • V is relatively omega-closed w.r.t. L.

Note 1: omega-admissibility of a controller implies an omega-nonblocking closed loop, i.e.:

Prefix(L)∩Prefix(H)  =  Prefix(L∩H)

Thus, the closed-loop behaviour under admissible control is adequately modelled by the intersection K := L∩H. The latter can be verified to be omega-admissible itself.

Note 2: omega-admissibility is retained under arbitrary unions. In particular, given a language inclusion specification E, the supremum

H↑ := sup{ H | L∩H ⊆ E, H is omega-admissible w.r.t. L }

exists uniquely and is omega-admissible itself. The supremal closed-loop behaviour is denoted K↑ := L∩H↑ and we have

K↑ = sup{ K ⊆ L∩E | K is omega-admissible w.r.t. L }

IoSynthesisNB

Controller synthesis for I/O systems (marked languages).

Signature:

IoSynthesisNB(+In+ IoSystem GPlant, +In+ Generator GSpec, +Out+ IoSystem GSupervisor)

Detailed description:

Given a plant L = Bm(GPlant) and a specification E = Bm(GSpec), this procedure computes a realisation of the supremal closed-loop behaviour under omega-admissible control, i.e.,
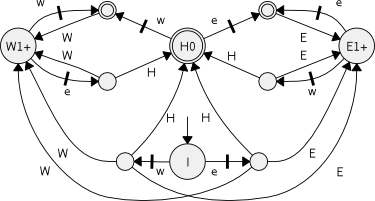
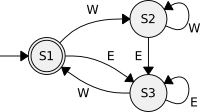
Bm(GSupervisor) = sup{ K ⊆ L∩E, K is omega-admissible w.r.t. L }

This implementation invokes OmegaSupConNB for the actual synthesis where Y are considered the uncontrollable events. The event attributes of the result are configured accordingly.

Example:

We give a variation of the vehicle example, with an alternative abstraction and specification, both involving liveness properties. Since the actual plant is an I/O system with an omega-free input the resulting controller is also admissible to the actual plant; see also IsIoSystem and IsInputOmegaFree.

Abstraction L' Specification E
     
Supervisor H
Parameter Conditions:

This implementation requires the alphabets of plant and specification to match. Furthermore, both generators must be deterministic. Effectively, the specification is intersected with the plant. The result will be deterministic and omega-trim.

IoSynthesis

Controller synthesis for I/O systems.

Signature:

IoSynthesis(+In+ IoSystem GPlant, +In+ Generator GSpec, +Out+ IoSystem GSupervisor)

Detailed description:

Given a plant L = B(GPlant) and a specification E = B(GSpec), this procedure computes a realisation of the supremal closed-loop behaviour under omega-admissible control, i.e., K↑ = B(GSupervisor). In contrast to IoSynthesisNB, this procedure operates on the generated languages and ignores any marking.

For omega-closed languages L and H, omega-admissibility is equivalent to

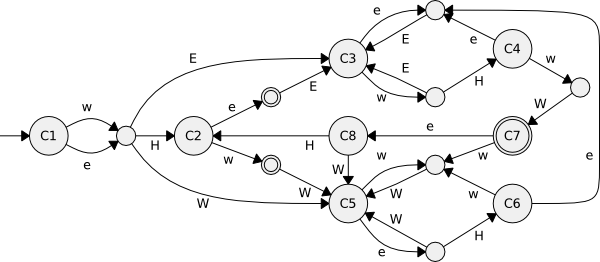
  • Prefix(L)∩Prefix(V) is controllable w.r.t. (Prefix(L),Y), and

  • L and H are locally nonblocking, i.e. Prefix(L)∩Prefix(H) is complete,

and, thus, SupConCmplClosed is invoked for the actual synthesis procedure.

Example:

The vehicle example has been synthesized with IoSynthesis. Since the actual plant is an I/O system with an omega-free input the resulting controller is also omega-admissible to the actual plant; see also IsIoSystem and IsInputOmegaFree.

Parameter Conditions:

This implementation requires the alphabets of plant and specification to match. Furthermore, both generators must be deterministic. Effectively, the specification is intersected with the plant. The result will be deterministic and accessible.

libFAUDES 2.32b --- 2024.03.08 --- with "synthesis-observer-diagnosis-iosystem-hiosys-multitasking-coordinationcontrol-timed-iodevice-simulator-luabindings"

>>