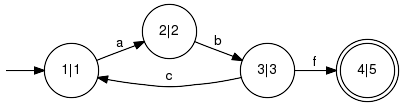
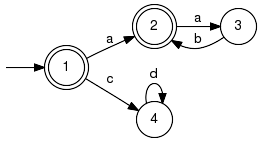
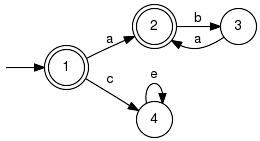
Boolean Operations on Languages

Functions on generators that perform set theoretic operations on languages, aka union, intersection and complement. Unless otherwise noted, semantics refer to the marked languages as opposed to the generated closed languages.

Note. The functions in this section ignore any attributes (controllability etc.) specified for the arguments. For the results, attributes are set to the default value. This may change in a future implementation.

LanguageUnion

Computes the union of languages.

Signature:

LanguageUnion(+In+ Generator G1, +In+ Generator G2, +Out+ Generator GRes)

LanguageUnion(+In+ GeneratorVector GVec, +Out+ Generator GRes)

Detailed description:

Computes a generator, which marks the union of the languages marked by the specified input generators. Moreover, the same is achieved for the involved generated (prefix-closed) languages:

Lm(G_Res) = Lm(G1) ∪ Lm(G2)      and      L(G_Res) = L(G1) ∪ L(G2).

The implementation first performs the textbook version in taking unions of all generator entities (alphabets, initial states, ...) and then post-processes the result in converting it to a deterministic generator. State sets are taken as disjoint by definition and thus are re-indexed and renamed to achieve disjoint union. The resulting language is defined over the union of the alphabets of the original languages; original languages defined over different alphabets are treated as if they were defined over the union of all input alphabets.

Example:
G1 G2


G_Res, Lm(G_Res) = Lm(G1) ∪ Lm(G2)
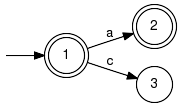
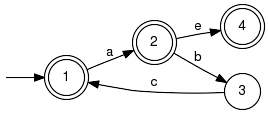
Parameter Conditions:

Input parameters may be non-deterministic. The implementation invokes Deterministic() to convert the result into a deterministic generator. Note that this conversion is usually straightforward, but there exist worst-case examples that manifest the exponential complexity.

LanguageIntersection

Computes the intersection of languages.

Signature:

LanguageIntersection(+In+ Generator G1, +In+ Generator G2, +Out+ Generator GRes)

LanguageIntersection(+In+ GeneratorVector GVec, +Out+ Generator GRes)

Detailed description:

Computes a generator, which marks the intersection of the languages marked by the specified input generators. Moreover, the same is achieved for the involved generated (prefix-closed) languages:

Lm(G_Res) = Lm(G1) ∩ Lm(G2)      and      L(G_Res) = L(G1) ∩ L(G2).

The resulting languages are defined over the intersection of the involved alphabets.

This function calls Product(). In the product of two automata, an event occurs if and only if it occurs in both automata rGen1 and rGen2. The result generates/marks the intersection of the involved languages, see e.g. [C2]

Example:
G1 G2


G_Res, Lm(G_Res) = Lm(G1) ∩ Lm(G2)
Parameter Conditions:

Input parameters may be non-deterministic. The result can be non-deterministic only if input parameters are non-deterministic.

LanguageComplement

Computes the complement of a language.

Signature:

LanguageComplement(+InOut+ Generator GPar)

LanguageComplement(+In+ Generator GArg, +Out+ Generator GRes)

LanguageComplement(+In+ Generator GArg, +In+ EventSet Sigma, +Out+ Generator GRes)

Detailed description:

Converts a generator marking the language Lm(G) into a generator marking the language complement w.r.t. the specified alphabet Sigma, i.e. Lm(G_Res) = Sigma*-Lm(G). The implementation calls Automaton() first and then inverts the marking of the states of the result:

Example:
G G_Res
Parameter Conditions:

The input generator must be deterministic. If not explicitly specified, the alphabet Sigma is taken from the input generator.

LanguageDifference

Computes the difference of two languages.

Signature:

LanguageDifference(+In+ Generator G1, +In+ Generator G2, +Out+ Generator GRes)

Detailed description:

Computes a generator that marks the set-difference of two marked languages Lm1 and Lm2:

Lm(G_Res) = Lm(G1) - Lm(G2).

The implementation first takes the complement of the second argument and then takes the intersection with the first. The complement is taken w.r.t. the alphabet of G1.

Example:
G1 G2


G_Res, Lm(G_Res) = Lm(G1) - Lm(G2)
Parameter Conditions:

The second argument is required to be a deterministic realisation. Provided the first argument is deterministic, too, the result is deterministic.

LanguageDisjoint

Tests whether two languages are disjoint.

Signature:

LanguageDisjoint(+In+ Generator G1, +In+ Generator G2, +Out+ Boolean BRes)

Detailed description:

Test whether the specified marked languages are disjoint, i.e. whether Lm(G1) ∩ Lm(G2)  =  0. The generated closed languages are not considered. The current implementation of this function traverses the set of synchronously reachable states until a pair of marked states is reached simultaneously.

Parameter Conditions:

Generators are required to be deterministic realisations of the respective languages.

LanguageEquality

Tests whether two languages are equal.

Signature:

LanguageEquality(+In+ Generator G1, +In+ Generator G2, +Out+ Boolean BRes)

Detailed description:

Test whether the specified marked languages are equal, i.e. whether Lm(G1)  =  Lm(G2). The generated closed languages are not considered. The current implementation of this function tests for mutual inclusion. Future implementations may be more efficient.

Parameter Conditions:

Generators are required to be deterministic realisations of the respective languages.

LanguageInclusion

Tests whether a languages includes another language.

Signature:

LanguageInclusion(+In+ Generator G1, +In+ Generator G2, +Out+ Boolean BRes)

Detailed description:

Test for Lm(G1)  ⊆  Lm(G2). The generated closed languages are not considered. The current implementation of this function computes the intersection Lm(G1) ∩ (Sigma*-Lm(G2)) and then tests for emptiness. Future implementations may be more efficient.

Parameter Conditions:

Generators are required to be deterministic realisations of the respective languages.

libFAUDES 2.32b --- 2024.03.08 --- with "synthesis-observer-diagnosis-iosystem-hiosys-multitasking-coordinationcontrol-timed-iodevice-simulator-luabindings"

>>