Omega Automata Plug-In

Detailed Description

The omega-automata plug-in collects data structures and functions to support supervisory control of non-termination processes.

License

The omega-automata plugin is distributed with libFAUDES and under the terms of the LGPL.

Copyright (c) 2025 Thomas Moor.

Classes
class	faudes::LabeledTree
class	faudes::RabinPair
class	faudes::RabinAcceptance

Functions
bool	faudes::IsBuechiControllable (const Generator &rGenPlant, const EventSet &rCAlph, const Generator &rGenCand)
bool	faudes::IsBuechiControllable (const System &rPlantGen, const Generator &rCandGen)
void	faudes::SupBuechiCon (const Generator &rPlantGen, const EventSet &rCAlph, const Generator &rSpecGen, Generator &rResGen)
void	faudes::SupBuechiCon (const System &rPlantGen, const Generator &rSpecGen, Generator &rResGen)
void	faudes::BuechiCon (const Generator &rPlantGen, const EventSet &rCAlph, const Generator &rSpecGen, Generator &rResGen)
void	faudes::BuechiCon (const System &rPlantGen, const Generator &rSpecGen, Generator &rResGen)
void	faudes::SupBuechiConNorm (const Generator &rPlantGen, const EventSet &rCAlph, const EventSet &rOAlph, const Generator &rSpecGen, Generator &rResGen)
void	faudes::SupBuechiConNorm (const System &rPlantGen, const Generator &rSpecGen, Generator &rResGen)
void	faudes::BuechiConNorm (const Generator &rPlantGen, const EventSet &rCAlph, const EventSet &rOAlph, const Generator &rSpecGen, Generator &rResGen)
void	faudes::BuechiConNorm (const System &rPlantGen, const Generator &rSpecGen, Generator &rResGen)
bool	faudes::BuechiTrim (vGenerator &rGen)
bool	faudes::BuechiTrim (const vGenerator &rGen, vGenerator &rRes)
void	faudes::BuechiProduct (const Generator &rGen1, const Generator &rGen2, Generator &rResGen)
void	faudes::aBuechiProduct (const Generator &rGen1, const Generator &rGen2, Generator &rResGen)
void	faudes::BuechiParallel (const Generator &rGen1, const Generator &rGen2, Generator &rResGen)
void	faudes::aBuechiParallel (const Generator &rGen1, const Generator &rGen2, Generator &rResGen)
void	faudes::BuechiClosure (Generator &rGen)
bool	faudes::IsBuechiClosed (const Generator &rGen)
void	faudes::ExportHoa (std::ostream &rOutStream, const Generator &rAut, SymbolTable *pSymTab)
void	faudes::ExportHoa (const std::string &rFilename, const Generator &rAut, SymbolTable *pSymTab)
void	faudes::ImportHoa (std::istream &rInStream, Generator &rGen, const SymbolTable *pSymTab, bool resolve, bool trace)
void	faudes::ImportHoa (const std::string &rFilename, Generator &rGen, const SymbolTable *pSymTab, bool resolve, bool trace)
void	faudes::PseudoDet (const RabinAutomaton &rGen, RabinAutomaton &rRes)
std::string	faudes::ComputeTreeSignature (const LabeledTree &tree, const std::set< int > &deletedNodes)
void	faudes::RemoveEps (const RabinAutomaton &rGen, RabinAutomaton &rRes)
void	faudes::RabinCtrlPfx (const RabinAutomaton &rRAut, const EventSet &rSigmaCtrl, StateSet &rCtrlPfx)
void	faudes::RabinCtrlPfx (const RabinAutomaton &rRAut, const EventSet &rSigmaCtrl, Generator &rResGen)
void	faudes::RabinCtrlPfx (const RabinAutomaton &rRAut, const EventSet &rSigmaCtrl, TaIndexSet< EventSet > &rController)
void	faudes::SupRabinCon (const Generator &rBPlant, const EventSet &rCAlph, const RabinAutomaton &rRSpec, RabinAutomaton &rRes)
void	faudes::SupRabinCon (const System &rBPlant, const RabinAutomaton &rRSpec, RabinAutomaton &rRes)
void	faudes::RabinCtrl (const Generator &rBPlant, const EventSet &rCAlph, const RabinAutomaton &rRSpec, Generator &rRes)
void	faudes::RabinCtrl (const System &rBPlant, const RabinAutomaton &rRSpec, Generator &rRes)
void	faudes::RabinCtrl (const Generator &rBPlant, const EventSet &rCAlph, const Generator &rGLSpec, const RabinAutomaton &rRUSpec, Generator &rRes)
void	faudes::RabinCtrl (const System &rBPlant, const Generator &rBLSpec, const RabinAutomaton &rRUSpec, Generator &rRes)
void	faudes::RabinCtrlPfxWithFeedback (const RabinAutomaton &rRAut, const EventSet &rSigmaCtrl, TaIndexSet< EventSet > &rController)
void	faudes::RabinLifeStates (const TransSet &rTransRel, const TransSetX2EvX1 &rRevTransRel, const RabinPair &rRPair, StateSet &rLife)
void	faudes::RabinLifeStates (const vGenerator &rRAut, const RabinPair &rRPair, StateSet &rLife)
void	faudes::RabinLifeStates (const RabinAutomaton &rRAut, StateSet &rLife)
bool	faudes::IsRabinLife (const RabinAutomaton &rRAut)
void	faudes::RabinTrimSet (const RabinAutomaton &rRAut, StateSet &rTrim)
bool	faudes::RabinTrim (RabinAutomaton &rRAut)
bool	faudes::RabinTrim (const RabinAutomaton &rRAut, RabinAutomaton &rRes)
bool	faudes::IsRabinTrim (const RabinAutomaton &rRAut)
void	faudes::RabinSimplify (RabinAutomaton &rRAut)
void	faudes::RabinSimplify (const RabinAutomaton &rRAut, RabinAutomaton &rRes)
void	faudes::RabinBuechiAutomaton (const RabinAutomaton &rRAut, const Generator &rBAut, RabinAutomaton &rRes)
void	faudes::RabinBuechiProduct (const RabinAutomaton &rRAut, const Generator &rBAut, RabinAutomaton &rRes)

Function Documentation

aBuechiParallel()

FAUDES_API void faudes::aBuechiParallel	(	const Generator &	rGen1,
		const Generator &	rGen2,
		Generator &	rResGen
	)

Parallel composition with relaxed acceptance condition.

See also BuechiParallel(const Generator&, const Generator&, Generator&). This version tries to be transparent on event attributes: if argument attributes match and if the result can take the respective attributes, then they are copied; it is considered an error if argument attributes do not match.

Parameters

rGen1	First generator
rGen2	Second generator
rResGen	Reference to resulting composition generator

Definition at line 525 of file omg_buechifnct.cpp.

aBuechiProduct()

FAUDES_API void faudes::aBuechiProduct	(	const Generator &	rGen1,
		const Generator &	rGen2,
		Generator &	rResGen
	)

Product composition for Buechi automata

See also BuechiProduct(const Generator&, const Generator&, Generator&). This version tries to be transparent on event attributes: if argument attributes match and if the result can take the respective attributes, then they are copied; it is considered an error if argument attributes do not match.

Parameters

rGen1	First generator
rGen2	Second generator
rResGen	Reference to resulting product composition generator

Definition at line 288 of file omg_buechifnct.cpp.

BuechiClosure()

FAUDES_API void faudes::BuechiClosure

(

Generator &

rGen

)

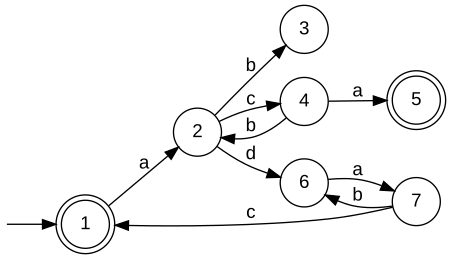
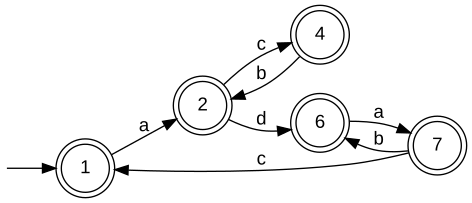
Topological closure.

This function computes the topological closure the omega language Bm accepted by the Buechi automaton rGen.

Method: First, BuechiTrim is called to erase all states of rGen that do not contribute to Bm. Then, all remaining states are marked.

No restrictions on parameter.

Parameters

rGen	Generator that realizes Bm to which omega closure is applied

Example:

Generator G	BuechiClosure(G)

Definition at line 70 of file omg_buechifnct.cpp.

BuechiCon() [1/2]

FAUDES_API void faudes::BuechiCon	(	const Generator &	rPlantGen,
		const EventSet &	rCAlph,
		const Generator &	rSpecGen,
		Generator &	rResGen
	)

Omega-synthesis w.r.t. Buechi accptance

This procedure first computes the supremal omega-controllable sublanguage as proposed by J. Thistle, 1992, applied to the specific case of deterministoc Buechi automata. It then applies a control pattern to obtain a relatively topologically-closed result, i.e., the topological closure of the result can be used as a supervisor.

Parameter restrictions: both generators must be deterministic and have the same alphabet.

Parameters

rPlantGen	Plant G
rCAlph	Controllable events
rSpecGen	Specification Generator E
rResGen	Reference to resulting Generator to realize the closed-loop behaviour.

Exceptions

Exception

alphabets of generators don't match (id 100) plant nondeterministic (id 201) spec nondeterministic (id 203) plant and spec nondeterministic (id 204)

Definition at line 1381 of file omg_buechictrl.cpp.

BuechiCon() [2/2]

FAUDES_API void faudes::BuechiCon	(	const System &	rPlantGen,
		const Generator &	rSpecGen,
		Generator &	rResGen
	)

Omega-synthesis

This is the RTI wrapper for
BuechiCon(const Generator&, const EventSet&, const Generator&, Generator&). Controllability attributes are taken from the plant argument. If the result is specified as a System, attributes will be copied from the plant argument.

Parameters

rPlantGen	Plant System
rSpecGen	Specification Generator
rResGen	Reference to resulting Generator to realize the closed-loop behaviour.

Exceptions

Exception

Alphabets of generators don't match (id 100) plant nondeterministic (id 201) spec nondeterministic (id 203) plant and spec nondeterministic (id 204)

Definition at line 1427 of file omg_buechictrl.cpp.

BuechiConNorm() [1/2]

FAUDES_API void faudes::BuechiConNorm	(	const Generator &	rPlantGen,
		const EventSet &	rOAlph,
		const EventSet &	rCAlph,
		const Generator &	rSpecGen,
		Generator &	rResGen
	)

Omega-synthesis for partial observation (experimental!)

Variation of supremal controllable prefix under partial observation. This variation applies a control pattern to obtain a relatively closed and omega-normal result. The latter properties are validated and an exception is thrown on an error. Thus, this function should not produce "false-positives". However, since it is derived from SupBuechiConNorm(), is may return the empty languages even if a non-empty controller exists.

Parameter restrictions: both generators must be deterministic and have the same alphabet.

Parameters

rPlantGen	Plant G
rCAlph	Controllable events
rOAlph	Observable events
rSpecGen	Specification Generator E
rResGen	Reference to resulting Generator to realize the supremal closed-loop behaviour.

Exceptions

Exception

alphabets of generators don't match (id 100) plant nondeterministic (id 201) spec nondeterministic (id 203) plant and spec nondeterministic (id 204)

Definition at line 1492 of file omg_buechictrl.cpp.

BuechiConNorm() [2/2]

FAUDES_API void faudes::BuechiConNorm	(	const System &	rPlantGen,
		const Generator &	rSpecGen,
		Generator &	rResGen
	)

Omega-synthesis for partial observation (experimental!)

This is the RTI wrapper for
BuechiConNorm(const Generator&, const EventSet&, const Generator&, Generator&). Controllability attributes are taken from the plant argument. If the result is specified as a System, attributes will be copied from the plant argument.

Parameters

rPlantGen	Plant System
rSpecGen	Specification Generator
rResGen	Reference to resulting Generator to realize the closed-loop behaviour.

Exceptions

Exception

Alphabets of generators don't match (id 100) plant nondeterministic (id 201) spec nondeterministic (id 203) plant and spec nondeterministic (id 204)

Definition at line 1548 of file omg_buechictrl.cpp.

BuechiParallel()

FAUDES_API void faudes::BuechiParallel	(	const Generator &	rGen1,
		const Generator &	rGen2,
		Generator &	rResGen
	)

Parallel composition with relaxed acceptance condition.

This version of the parallel composition relaxes the synchronisation of the acceptance condition (marking). It requires that the omega extension of the generated language has infinitely many prefixes that comply to the marked languages of G1 and G2, referring to the projection on the respective alphabet. It does however not require the synchronous acceptance.

Parameters

rGen1	First generator
rGen2	Second generator
rResGen	Reference to resulting parallel composition generator

Definition at line 316 of file omg_buechifnct.cpp.

BuechiProduct()

FAUDES_API void faudes::BuechiProduct	(	const Generator &	rGen1,
		const Generator &	rGen2,
		Generator &	rResGen
	)

Product composition for Buechi automata

Referring to the Buechi acceptance condition, the resulting genarator accepts all those inifinite words that are accepted by both, G1 and G2. This implementation extends the usual product state space by a flag to indentify executions with alternating marking.

Parameters

rGen1	First generator
rGen2	Second generator
rResGen	Reference to resulting product composition generator

Definition at line 166 of file omg_buechifnct.cpp.

BuechiTrim() [1/2]

FAUDES_API bool faudes::BuechiTrim	(	const vGenerator &	rGen,
		vGenerator &	rRes
	)

Trim generator w.r.t Buechi acceptance

This is a API wrapper for BuechiTrim(vGenerator&).

Parameters

rGen	Automaton to trim (const ref)
rRes	Resulting automaton

Returns

True if resulting generator contains at least one initial state and at least one marked state.

Definition at line 54 of file omg_buechifnct.cpp.

BuechiTrim() [2/2]

FAUDES_API bool faudes::BuechiTrim

(

vGenerator &

rGen

)

Trim generator w.r.t Buechi acceptance

This function removes states such that the generator becomes omega trim while not affecting the induced omega language.

The implementation first makes the generator accessible and then iteratively removes state that either never reach a marked state or that are guaranteed to eventually reach a terminal state. There might be a more efficient approach.

Parameters

rGen	Automaton to trim

Returns

True if resulting generator contains at least one initial state and at least one marked state.

Definition at line 34 of file omg_buechifnct.cpp.

ComputeTreeSignature()

FAUDES_API std::string faudes::ComputeTreeSignature	(	const LabeledTree &	tree,
		const std::set< int > &	deletedNodes
	)

Compute tree signature for state equivalence checking (Enhanced)

Parameters

tree	Input labeled tree
deletedNodes	Set of deleted node numbers

Returns

String signature representing the tree structure and deleted nodes

Definition at line 203 of file omg_pseudodet.cpp.

ExportHoa() [1/2]

FAUDES_API void faudes::ExportHoa	(	const std::string &	rFilename,
		const Generator &	rAut,
		SymbolTable *	pSymTab = nullptr
	)

Export Automaton as HOA formated stream

Convenience wrapper, for detail see ExportHoa(std::ostream&, const Generator&)

Parameters

rFilename	File to write to
rAut	Automaton to write
pSymTab	Optional symbol table to record event mapping

Definition at line 204 of file omg_hoa.cpp.

ExportHoa() [2/2]

FAUDES_API void faudes::ExportHoa	(	std::ostream &	rOutStream,
		const Generator &	rAut,
		SymbolTable *	pSymTab = nullptr
	)

Export Automaton as HOA formated stream

We iterate over all relevant entities of the specified automaton and somewhat adboc writes HOA formated entities to the specified stream.

Our current implementation uses dynamic cast to figure wheter to to output a Buechi or a Rabin automaton

Parameters

rOutStream	Stream to write to
rAut	Automaton to write
pSymTab	Optional symbol table to record event mapping

Definition at line 187 of file omg_hoa.cpp.

ImportHoa() [1/2]

FAUDES_API void faudes::ImportHoa	(	const std::string &	rFilename,
		Generator &	rGen,
		const SymbolTable *	pSymTab = nullptr,
		bool	resolve = false,
		bool	trace = false
	)

Import Automaton from HOA formated file

Convenience wrapper, see ImportHoa(std::istream&,RabinAutomaton&) for details.

Parameters

rFilename	File to read from
rGen	Resultimg automaton
pSymTab	Optional symbol table to provide event mapping
resolve	Ask cpphoafparser to resolve aliases
trace	Ask cpphoafparser for a parse trace on std::cerr

Definition at line 530 of file omg_hoa.cpp.

ImportHoa() [2/2]

FAUDES_API void faudes::ImportHoa	(	std::istream &	rInStream,
		Generator &	rGen,
		const SymbolTable *	pSymTab = nullptr,
		bool	resolve = false,
		bool	trace = false
	)

Import Automaton from HOA formated stream

To reading input in HAO format we use the cpphoafparser library, authored/copyrighted by

Joachim Klein klein.nosp@m.@tcs.nosp@m..inf..nosp@m.tu-d.nosp@m.resde.nosp@m.n.de David Mueller david.nosp@m..mue.nosp@m.ller@.nosp@m.tcs..nosp@m.inf.t.nosp@m.u-dr.nosp@m.esden.nosp@m..de

We have found the original sources at

http://automata.tools/hoa/cpphoafparser

They are distributed under LGPL v2.1 conditions and we include them with libFAUDES under the same license terms.

Our current implementation can read Rabin and Buechi automata, preferably with implicit edges. This is not a restriction of cpphoafparser and may be extended for further use cases in future.

Parameters

rInStream	Stream to read from
rGen	Resultimg automaton
pSymTab	Optional symbol table to provide event mapping
resolve	Ask cpphoafparser to resolve aliase
trace	Ask cpphoafparser for a parse trace on std::cerr

Definition at line 503 of file omg_hoa.cpp.

IsBuechiClosed()

FAUDES_API bool faudes::IsBuechiClosed

(

const Generator &

rGen

)

Test for topologically closed omega language.

This function tests whether the omega language Bm(G) realized by the specified Buechi automata is topologically closed.

Method: First, compute the Buechi-trim state set and restrict the discussion to that set. Then, omega-closedness is equivalent to the non-existence on a non-trivial SCC with no marked states.

Parameters

rGen	Generator that realizes Bm to which omega closure is applied

Returns

True <> Bm(G) is omega closed

Definition at line 84 of file omg_buechifnct.cpp.

IsBuechiControllable() [1/2]

FAUDES_API bool faudes::IsBuechiControllable	(	const Generator &	rPlantGen,
		const EventSet &	rCAlph,
		const Generator &	rSupCandGen
	)

Test omega controllability

Tests whether the candidate supervisor H is omega controllable w.r.t. the plant G, where omega-languages are interpreted by Buechi acceptance condition. This implementation invokes IsControllable and IsBuechiRelativelyClosed. A future implementation may be more efficient.

Parameter restrictions: both generators must be deterministic, omega-trim and have the same alphabet.

Parameters

rPlantGen	Plant G
rCAlph	Controllable events
rSupCandGen	Supervisor candidate H

Exceptions

Exception

Alphabets of generators don't match (id 100) Arguments are not omega trim (id 201, only if FAUDES_CHECKED is set) Arguments are non-deterministic (id 202, only if FAUDES_CHECKED is set)

Returns

true / false

Definition at line 40 of file omg_buechictrl.cpp.

IsBuechiControllable() [2/2]

FAUDES_API bool faudes::IsBuechiControllable	(	const System &	rPlantGen,
		const Generator &	rSupCandGen
	)

Test omega-controllability.

Tests whether the candidate supervisor h is omega controllable w.r.t. the plant g; this is a System wrapper for IsOmegaControllable.

Parameters

rPlantGen	Plant g generator
rSupCandGen	Supervisor candidate h generator

Exceptions

Exception

Alphabets of generators don't match (id 100) Arguments are not omega trim (id 201, only if FAUDES_CHECKED is set) Arguments are non-deterministic (id 202, only if FAUDES_CHECKED is set)

Returns

true / false

Definition at line 105 of file omg_buechictrl.cpp.

IsRabinLife()

FAUDES_API bool faudes::IsRabinLife

(

const RabinAutomaton &

rRAut

)

Test for lifeness w.r.t a Rabin acceptance condition.

Returns true iff all accessible states are life.

Parameters

rRAut

Trasition system to operate on

Returns

trud iff Rabin automaton is life.

Definition at line 145 of file omg_rabinfnct.cpp.

IsRabinTrim()

FAUDES_API bool faudes::IsRabinTrim

(

const RabinAutomaton &

rRAut

)

Test a Rabinautomaton to be trim.

Returns true iff all states are accessible and life.

Parameters

rRAut

Trasition system to operate on

Returns

trud iff Rabin automaton is life.

Definition at line 180 of file omg_rabinfnct.cpp.

PseudoDet()

FAUDES_API void faudes::PseudoDet	(	const RabinAutomaton &	rGen,
		RabinAutomaton &	rRes
	)

Pseudo-determinization algorithm for Rabin automata (Paper Algorithm)

This function converts a nondeterministic Rabin automaton to an equivalent deterministic Rabin automaton using the pseudo-determinization algorithm from the paper, with fixed node numbering and enhanced state tracking.

Parameters

rGen	Input nondeterministic Rabin automaton

Returns

Equivalent deterministic Rabin automaton

Exceptions

Exception

Input automaton has no initial states (id 201) Algorithm complexity limits exceeded (id 202)

Definition at line 248 of file omg_pseudodet.cpp.

RabinBuechiAutomaton()

FAUDES_API void faudes::RabinBuechiAutomaton	(	const RabinAutomaton &	rRAut,
		const Generator &	rBAut,
		RabinAutomaton &	rRes
	)

Construct Rabin-Buechi automata.

Given two automata rRAut and rBAut, this function constructs the accessible product state set and corresponding syncronizsed transitions. For the generated languages, this is exactly the same as the common product operation. It then lifts the two individual acceptance conditions to the product state set. If both rRAut and rBAut are full, so is the result. In that case, the result accepts by its Rabin acceptance condition runs that are accepted by rRAut and by its Buechi acceptance condition those path thet are accepted by rBAut.

The intended use case is when rRAut is a lifeness specification and rBAut is a plant with lifeness guarantees.

Parameters

rRAut	Rabin automaton
rBAut	Buechi automaton
rRes	Resulting product automaton

Definition at line 215 of file omg_rabinfnct.cpp.

RabinBuechiProduct()

FAUDES_API void faudes::RabinBuechiProduct	(	const RabinAutomaton &	rRAut,
		const Generator &	rBAut,
		RabinAutomaton &	rRes
	)

Product composition for a Rabin automaton with a Buechi automaton

Referring to each acceptance condition specified by rRAut and rBAut, the resulting Rabin automaton accepts all those runs, that are accepted by both rRAut and rBAut. To support supervisory control, this function sets the marking of the result as a lifted variant of rBAut.

This implementation extends the usual product state space by a flag to indentify executions with alternating marking. This restricts the applicability to one Rabin pair only. Future revisions may drop this restriction.

Parameters

rRAut	First automaton
rBAut	Second automaton
rRes	Reference to resulting product composition

Definition at line 301 of file omg_rabinfnct.cpp.

RabinCtrl() [1/4]

FAUDES_API void faudes::RabinCtrl	(	const Generator &	rBPlant,
		const EventSet &	rCAlph,
		const Generator &	rGLSpec,
		const RabinAutomaton &	rRUSpec,
		Generator &	rRes
	)

Omega-synthesis w.r.t. Buechi/Rabin acceptance condition

Computation of a controller that respects next to the common upper bound specification also a lower bound. Only on exit of the lower-bound, the greedy controlle is activated. The result returned is a Buechi automaton of the closed-loop behaviour. The closure is readily utilised as a controller.

Parameter restrictions: both generators must be deterministic and refer to the same alphabet. The lower bound argument is interpreted as the generated omega-language intersected with the plant behaviour. The effective lower bound must not exceed the supremal omega-controllable sublanguage of the upper bound specification. This is currently not checked.

Parameters

rBPlant	Plant to accept L w.r.t. Buechi acceptance
rGLSpec	Specification to be generate the lower bound A
rRUSpec	Specification to accept the upper bound E w.r.t. Rabin acceptance
rRes	Closed-loop behaviour.

Exceptions

Exception

alphabets of generators don't match (id 100) plant nondeterministic (id 201) spec nondeterministic (id 203) plant and spec nondeterministic (id 204)

Definition at line 810 of file omg_rabinctrl.cpp.

RabinCtrl() [2/4]

FAUDES_API void faudes::RabinCtrl	(	const Generator &	rBPlant,
		const EventSet &	rCAlph,
		const RabinAutomaton &	rRSpec,
		Generator &	rRes
	)

Omega-synthesis w.r.t. Buechi/Rabin acceptance condition

Computation of the "greedy" controller that runs for early acceptance. The result is a Buechi automaton of the closed-loop behaviour under greedy control. The closure is readily utilised as a controller.

Parameter restrictions: both generators must be deterministic and refer to the same alphabet.

Parameters

rBPlant	Plant to accept L w.r.t. Buechi acceptance
rCAlph	Controllable events
rRSpec	Specification to accept E w.r.t. Rabin acceptance
rRes	Closed-loop behaviour under greedy control.

Exceptions

Exception

alphabets of generators don't match (id 100) plant nondeterministic (id 201) spec nondeterministic (id 203) plant and spec nondeterministic (id 204)

Definition at line 749 of file omg_rabinctrl.cpp.

RabinCtrl() [3/4]

FAUDES_API void faudes::RabinCtrl	(	const System &	rBPlant,
		const Generator &	rGLSpec,
		const RabinAutomaton &	rRUSpec,
		Generator &	rRes
	)

Omega-synthesis w.r.t. Buechi/Rabin acceptance condition

Computation of a controller that respects next to the common upper bound specification also a lower bound. Only on exit of the lower-bound, the greedy controlle is activated. This is an API wrapper to obtain controllability attributes from the plant parameter. The result returned is a Buechi automaton of the closed-loop behaviour. The closure is readily utilised as a controller.

Parameter restrictions: both generators must be deterministic and refer to the same alphabet. The lower bound argument is interpreted as the generated omega-language intersected with the plant behaviour. The effective lower bound must not exceed the supremal omega-controllable sublanguage of the upper bound specification. This is currently not checked.

Parameters

rBPlant	System to accept L w.r.t. Buechi acceptance
rGLSpec	Specification to be generate the lower bound A
rRUSpec	Specification to accept the upper bound E w.r.t. Rabin acceptance
rRes	Closed-loop behaviour.

Exceptions

Exception

alphabets of generators don't match (id 100) plant nondeterministic (id 201) spec nondeterministic (id 203) plant and spec nondeterministic (id 204)

Definition at line 941 of file omg_rabinctrl.cpp.

RabinCtrl() [4/4]

FAUDES_API void faudes::RabinCtrl	(	const System &	rBPlant,
		const RabinAutomaton &	rRSpec,
		Generator &	rRes
	)

Omega-synthesis w.r.t. Buechi/Rabin acceptance condition

Computation of the "greedy" supervisor that runs for early acceptance; this variant retrieves controllabillity arguments from the specified plant. The result is a Buechi automaton of the closed-loop behaviour under greedy control. The closure is readily utilised as a controller.

Parameter restrictions: both generators must be deterministic and refer to the same alphabet.

Parameters

rBPlant	Plant to accept L w.r.t. Buechi acceptance
rRSpec	Specification to accept E w.r.t. Rabin acceptance
rRes	Closed-loop behaviour udner greedy control.

Exceptions

Exception

alphabets of generators don't match (id 100) plant nondeterministic (id 201) spec nondeterministic (id 203) plant and spec nondeterministic (id 204)

Definition at line 919 of file omg_rabinctrl.cpp.

RabinCtrlPfx() [1/3]

FAUDES_API void faudes::RabinCtrlPfx	(	const RabinAutomaton &	rRAut,
		const EventSet &	rSigmaCtrl,
		Generator &	rCtrlPfx
	)

Controllability prefix for Rabin automata.

API wrapper to return the controllability prefix as generator.

Parameters

rRAut	Automaton to control
rSigmaCtrl	Set of controllable events
rCtrlPfx	Generator that marks the controllability prefix.

Definition at line 600 of file omg_rabinctrl.cpp.

RabinCtrlPfx() [2/3]

FAUDES_API void faudes::RabinCtrlPfx	(	const RabinAutomaton &	rRAut,
		const EventSet &	rSigmaCtrl,
		StateSet &	rCtrlPfx
	)

Controllability prefix for Rabin automata.

Computation of the controllability prefix as proposed by Thistle/Wonham in "Supervision of infinite behavior of Discrete Event Systems, 1994, using the fixpoint iteration from "Control of w-Automata, Church's Problem, and the Emptiness Problem for Tree w-Automata", 1992.

Parameters

rRAut	Automaton to control
rSigmaCtrl	Set of controllable events
rCtrlPfx	State set that marks the controllability prefix.

Definition at line 555 of file omg_rabinctrl.cpp.

RabinCtrlPfx() [3/3]

FAUDES_API void faudes::RabinCtrlPfx	(	const RabinAutomaton &	rRAut,
		const EventSet &	rSigmaCtrl,
		TaIndexSet< EventSet > &	rController
	)

Controllability prefix for Rabin automata.

API wrapper to return a controller

Parameters

rRAut	Automaton to control
rSigmaCtrl	Set of controllable events
rController	Map from states to enabled events.

Definition at line 576 of file omg_rabinctrl.cpp.

RabinCtrlPfxWithFeedback()

FAUDES_API void faudes::RabinCtrlPfxWithFeedback	(	const RabinAutomaton &	rRAut,
		const EventSet &	rSigmaCtrl,
		TaIndexSet< EventSet > &	rController
	)

Controllability prefix with state feedback for Rabin automata.

Extended version that computes both the controllability prefix and the corresponding state feedback controller, implementing Theorem 6.4 from Thistle/Wonham 1994.

Parameters

rRAut	Automaton to control
rSigmaCtrl	Set of controllable events
rCtrlPfx	State set that marks the controllability prefix
rStateFeedback	State feedback mapping: for each controllable state, provides the control pattern

Definition at line 732 of file omg_rabinctrlrk.cpp.

RabinLifeStates() [1/3]

FAUDES_API void faudes::RabinLifeStates	(	const RabinAutomaton &	rRAut,
		StateSet &	rLife
	)

Life states w.r.t a Rabin acceptance condition.

Iterates over all Rabin pairs and Returns the union of all life states.

Parameters

rRAut	Trasition system to operate on
rLife	Resulting set of life states

Definition at line 126 of file omg_rabinfnct.cpp.

RabinLifeStates() [2/3]

void faudes::RabinLifeStates	(	const TransSet &	rTransRel,
		const TransSetX2EvX1 &	rRevTransRel,
		const RabinPair &	rRPair,
		StateSet &	rLife
	)

Life states w.r.t a Rabin pair.

A state is considered life if it allows for a future path that such that the acceptance condition is met,

The implementation is along the following line

• initialise LSet the ISet
• run a nu iteration on LSet to figure the largest existential invariant
• run a mu iteration on LSet*RSet to restrict LSet to states which can reach RSet
• repeat the last to steps until a fix point is attained
• run one more mu iteration on LSet to extend to the bachward reach

Parameters

rTransRel	Trasition systej to operate on
rRevTransRel	Reverse sorted variant
rRPair	Rabin pair to consider
rLife	Resulting set of life states

Definition at line 34 of file omg_rabinfnct.cpp.

RabinLifeStates() [3/3]

FAUDES_API void faudes::RabinLifeStates	(	const vGenerator &	rRAut,
		const RabinPair &	rRPair,
		StateSet &	rLife
	)

Life states w.r.t a Rabin pair.

API wrapper.

Parameters

rRAut	Trasition system to operate on
rRPair	Rabin pair to consider
rLife	Resulting set of life states

Definition at line 111 of file omg_rabinfnct.cpp.

RabinSimplify() [1/2]

FAUDES_API void faudes::RabinSimplify	(	const RabinAutomaton &	rRAut,
		RabinAutomaton &	rRes
	)

Simplify Rabin acceptance condition

Simplify Rabin pairs while maintaining the accepted laguage.

Parameters

rRAut	Automaton to simplify
rRes	Resulting automaton

Definition at line 208 of file omg_rabinfnct.cpp.

RabinSimplify() [2/2]

FAUDES_API void faudes::RabinSimplify

(

RabinAutomaton &

rRAut

)

Simplify Rabin acceptance condition

Simplify Rabin pairs while maintaining the accepted laguage.

Parameters

rRAut

Automaton to simplify

Definition at line 189 of file omg_rabinfnct.cpp.

RabinTrim() [1/2]

FAUDES_API bool faudes::RabinTrim	(	const RabinAutomaton &	rRAut,
		RabinAutomaton &	rRes
	)

Trim generator w.r.t Rabin acceptance

Restrict the automaton to the set of trim states; see also RaibLifeStates and RabinTrimSet

Parameters

rRAut	Automaton to trim
rRes	Resulting trimmed automaton

Returns

True if resulting generator contains at least one initial state.

Definition at line 173 of file omg_rabinfnct.cpp.

RabinTrim() [2/2]

FAUDES_API bool faudes::RabinTrim

(

RabinAutomaton &

rRAut

)

Trim generator w.r.t Rabin acceptance

Restrict the automaton to the set of trim states; see also RaibLifeStates and RabinTrimSet

Parameters

rRAut

Automaton to trim

Returns

True if resulting generator contains at least one initial state.

Definition at line 162 of file omg_rabinfnct.cpp.

RabinTrimSet()

FAUDES_API void faudes::RabinTrimSet	(	const RabinAutomaton &	rRAut,
		StateSet &	rTrim
	)

Trim generator w.r.t. Rabin acceptance

This function computes the set of states that contribute to the accepted omega language. The current implementation returns the union of all states that are life w.r.t. a Rabin pair, restricted to reachable states.

Parameters

rRAut	Automaton to consider
rInv	Resulting set of trim statess

Definition at line 153 of file omg_rabinfnct.cpp.

RemoveEps()

FAUDES_API void faudes::RemoveEps	(	const RabinAutomaton &	rGen,
		RabinAutomaton &	rRes
	)

Remove epsilon transitions from a Rabin automaton

This function removes epsilon transitions from a Rabin automaton by:

1. Removing epsilon self-loops
2. Merging epsilon transitions with other transitions

Parameters

rGen	Input Rabin automaton with epsilon transitions
rRes	Output Rabin automaton without epsilon transitions

Definition at line 733 of file omg_pseudodet.cpp.

SupBuechiCon() [1/2]

FAUDES_API void faudes::SupBuechiCon	(	const Generator &	rPlantGen,
		const EventSet &	rCAlph,
		const Generator &	rSpecGen,
		Generator &	rResGen
	)

Omega-synthesis w.r.t. Buechi acceptance condition

Computation of the supremal oemga-controllable sublanguage as proposed by Thistle/Wonham in "Control of w-Automata, Church's Problem, and the Emptiness Problem for Tree w-Automata", 1992, and, here, applied to the specific case of deterministic Buechi automata. In the given setting, the result matches the limit of the controllable prefix intersected with the plant and specification omega-languages.

Parameter restrictions: both generators must be deterministic and refer to the same alphabet.

Parameters

rPlantGen	Plant G
rCAlph	Controllable events
rSpecGen	Specification Generator E
rResGen	Reference to resulting Generator to realize the supremal closed-loop behaviour.

Exceptions

Exception

alphabets of generators don't match (id 100) plant nondeterministic (id 201) spec nondeterministic (id 203) plant and spec nondeterministic (id 204)

Definition at line 1342 of file omg_buechictrl.cpp.

SupBuechiCon() [2/2]

FAUDES_API void faudes::SupBuechiCon	(	const System &	rPlantGen,
		const Generator &	rSpecGen,
		Generator &	rResGen
	)

Omega-synthesis w.r.t. Buechi acceptance

This is the RTI wrapper for
SupBuchiCon(const Generator&, const EventSet&, const Generator&, Generator&). Controllability attributes are taken from the plant argument. If the result is specified as a System, attributes will be copied from the plant argument.

Parameters

rPlantGen	Plant System
rSpecGen	Specification Generator
rResGen	Reference to resulting Generator to realize the supremal closed-loop behaviour.

Exceptions

Exception

Alphabets of generators don't match (id 100) plant nondeterministic (id 201) spec nondeterministic (id 203) plant and spec nondeterministic (id 204)

Definition at line 1360 of file omg_buechictrl.cpp.

SupBuechiConNorm() [1/2]

FAUDES_API void faudes::SupBuechiConNorm	(	const Generator &	rPlantGen,
		const EventSet &	rCAlph,
		const EventSet &	rOAlph,
		const Generator &	rSpecGen,
		Generator &	rResGen
	)

Omega-synthesis for partial observation (experimental!)

Variation of supremal omega-controllable sublanguage to address normality requirements in the context of partial observation. The test used in this implementation is sufficient but presumably to necessary. Thus, the function in general return only a subset of the relevant controllable prefix.

Parameter restrictions: both generators must be deterministic and have the same alphabet.

Parameters

rPlantGen	Plant G
rCAlph	Controllable events
rOAlph	Observable events
rSpecGen	Specification Generator E
rResGen	Reference to resulting Generator to realize the supremal closed-loop behaviour.

Exceptions

Exception

alphabets of generators don't match (id 100) plant nondeterministic (id 201) spec nondeterministic (id 203) plant and spec nondeterministic (id 204)

Definition at line 1450 of file omg_buechictrl.cpp.

SupBuechiConNorm() [2/2]

FAUDES_API void faudes::SupBuechiConNorm	(	const System &	rPlantGen,
		const Generator &	rSpecGen,
		Generator &	rResGen
	)

Omega-synthesis for partial observation (experimental!)

This is the RTI wrapper for
SupBuechiConNorm(const Generator&, const EventSet&, const Generator&, Generator&). Controllability attributes and observability attributes are taken from the plant argument. If the result is specified as a System, attributes will be copied from the plant argument.

Parameters

rPlantGen	Plant System
rSpecGen	Specification Generator
rResGen	Reference to resulting Generator to realize the supremal closed-loop behaviour.

Exceptions

Exception

Alphabets of generators don't match (id 100) plant nondeterministic (id 201) spec nondeterministic (id 203) plant and spec nondeterministic (id 204)

Definition at line 1471 of file omg_buechictrl.cpp.

SupRabinCon() [1/2]

FAUDES_API void faudes::SupRabinCon	(	const Generator &	rBPlant,
		const EventSet &	rCAlph,
		const RabinAutomaton &	rRSpec,
		RabinAutomaton &	rRes
	)

Omega-synthesis w.r.t. Buechi/Rabin acceptance condition

Computation of the supremal oemga-controllable sublanguage as proposed by Thistle/Wonham in "Control of w-Automata, Church's Problem, and the Emptiness Problem for Tree w-Automata", 1992, and, here, applied to the specific case of deterministic Buechi plangt and a Rabin specification.

Parameter restrictions: both generators must be deterministic and refer to the same alphabet.

Parameters

rBPlant	Plant to accept L w.r.t. Buechi acceptance
rCAlph	Controllable events
rRSpec	Specification to accept E w.r.t. Rabin acceptance
rRes	Resulting RabinAutomaton to accept the supremal controllable sunlanguage

Exceptions

Exception

alphabets of generators don't match (id 100) plant nondeterministic (id 201) spec nondeterministic (id 203) plant and spec nondeterministic (id 204)

Definition at line 657 of file omg_rabinctrl.cpp.

SupRabinCon() [2/2]

FAUDES_API void faudes::SupRabinCon	(	const System &	rBPlant,
		const RabinAutomaton &	rRSpec,
		RabinAutomaton &	rRes
	)

Omega-synthesis w.r.t. Buechi acceptance

This is the RTI wrapper for
SupRabinCon(const Generator&, const EventSet&, const Generator&, Generator&). Controllability attributes are taken from the plant argument. Attributes will be copied from the plant argument.

Parameters

rBPlant	System to accept L w.r.t. Buechi acceptance
rRSpec	Specification to accept E w.r.t. Rabin acceptance
rResGen	Reference to resulting RabinAutomaton to accept the supremal controllable sunlanguage

Exceptions

Exception

Alphabets of generators don't match (id 100) plant nondeterministic (id 201) spec nondeterministic (id 203) plant and spec nondeterministic (id 204)

Definition at line 697 of file omg_rabinctrl.cpp.