| |
|
|||||
|
|
||||||
Case Study: Flexible Manufacturing System

Our laboratory model of a flexible manufacturing system represents a prototypical scenario of industrial automation. It serves as a platform to guide our work in the area of discrete event systems and to evaluate the outcomes. The plant layout was originally designed by Hans Reger and Klaus Schmidt in 2003, and assembled by Staudinger GmbH. As of 2011, we also provide a simulator that mimics the dynamic behaviour of our laboratory model; see Manufacturing System Simulator.
Experimental Setup
The laboratory setup consists of 29 electro-mechanical components: 1 stack feeder (SF), 16 conveyor belts (C), 4 rotary tables (T), 2 rail-transport units (R), 2 processing stations (M), 2 pushers (P) and 2 roll-conveyors (RC). It is controlled by 107 digital signals, where 50 plant inputs operate 25 DC Motors in either direction and 57 plant outputs read switch-keys and inductive sensors.

The digital signals may either be wired to a programmable logic controller (PLC) or to a standard PC equipped with a digital IO board. In the former case, controller dynamics are encoded by a PLC program. In the latter case, we use libFAUDES as a software environment to sense/generate events from digital signals and to implement controller dynamics specified by finite automata; see also simfaudes. Both configurations establish a closed-loop system in which plant dynamics interact with controller dynamics to satisfy a closed-loop specification.
Plant Simulation
Whilst an actual physical plant is instructive for adequate modelling and rigoruos controller design, possible variations of the scenario are limited or come at a prohibitiv cost. For this reason, we have implemented a simulator to mimique the physical plant behaviour on signal level. It supports essentially the same closed-loop configurations as the laboratory experiment in that it either connects to a PLC as a Modbus/TCP slave or synchronizes with libFAUDES based controller dynamics. For fetailed information, incl. download- and installation-instructions, see Flexible Manufacturing System Simulator.
Automata Models

In order to apply research results from discrete event systems theory to the manufacturing system, we require a formal model of the plant dynamics. Here, we focus attention on the rotary table (T) to illustrate the modelling process.
The rotary table has two defined positions (x-position and y-position) that are indicated by switch-keys. A DC motor can be activated via two distinct digital signals for either clockwise or counterclockwise operation, directing the table towards the y- and x-position, respectively. Thus, a model of the rotary table dynamics may refer to the following events:
| event | semantics | signals |
|---|---|---|
| tmvx | move towards the the x-position | activate counterclockwise rotation |
| tmvy | move towards the the y-position | activate clockwise rotation |
| ts | stop moving | turn motor of |
| tax | arrive at x-position | positive edge of corresponding switch-key |
| tlx | leave x-position | negative edge of corresponding switch-key |
| tay | arrive at y-position | positive edge of corresponding switch-key |
| tly | leave y-position | negative edge of corresponding switch-key |
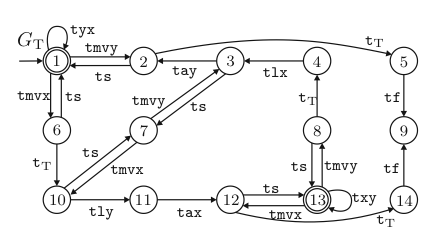
A model of the rotary table dynamics must distinguish event sequences that may occur from those that can not occur. Thus, we may use automata and formal languages to as a formal representation. In addition to the actuator- and sensor-events defined above, the automata model G_T of the rotary table introduces the logic events t_T, tf, and txy and tyx. The event t_T is used to model the time it takes to overrun a switch-key, which in turn issues the undesired failure event tf. It is the controllers task to stop the motor in time in order to prevent tf. The aditional events txy and tyx indicate that the respective rotation has been completed and facilitate a hierarchical controller design.
The remaining components are modelled accordingly and we end up with 29 automata models, ranging from 3 to 34 states, each.
| component | #states | #sensors | #actuators | #logic ev. |
|---|---|---|---|---|
| stack feeder (SF) | 14 | 4 | 2 | 1 |
| conveyor belt (C) | 28 | 3 | 3 | 4 |
| rotary table (T) | 14 | 4 | 3 | 1 |
| rail-transport unit (R) | 34 | 10 | 3 | 10 |
| processing station (M) | 34 | 4 | 5 | 2 |
| pusher (P) | 16 | 5 | 3 | 2 |
| roll-conveyors (RC) | 3 | 3 | 0 | 1 |
Hierarchical Controller Design
A single automaton (monolithic model), that represents the overall plant dynamics and, hence, refers to the product state space, and has approx. 10^24 states. Thus, explicit enumeration of the overall state space is regarded not feasible. This is a typical situation for realistic applications in an industrial automation context.
In order to circumvent the explicit composition of a monolithic model, various hierarchical design methods have been proposed in the literature. These methods first design local controllers on a per component basis to form the lowest level of a controller hierarchy. Then, small groups of components are composed as a basis for the controller design in the second level of the hierarchy. An abstraction step reduces the complexity in that it removes details of the model that are only relevant to the low-level controllers. The process is repeated until a single controller forms the top level of the hierarchy.
For the laboratory setup, we applied a hierarchical design method proposed by our group; see Schmidt, K., Moor, T., Perk, S., "Nonblocking Hierarchical Control of Decentralized Discrete Event Systems", IEEE Transactions on Automatic Control, vol. 53, no. 10, pp. 2252-2265, 2008; and Moor T., Schmidt K., Perk S., "Applied supervisory control for a flexible manufactoring system", WODES 2010, pp. 263-268, 2010 [PDF]. The design results in 39 controllers with an average of about 100 states arranged on 5 hierarchical levels. Further details, including component models and synthesis scripts, are provided in the user reference of the libFAUDES observer plug-in.